Problem:
In a certain circle, the chord of a d-degree arc is 22 centimeters longer than the chord of a 3d-degree arc, where d<120. The length of the chord of a 3d-degree arc is −m+n​ centimeters, where m and n are positive integers. Find m+n.
Solution:
In the figure, points A,B,C, and D are concyclic, the degree sizes of arcs AB,BC, and CD are all d, and AB=BC=CD=22. Note that AD is the chord of a 3d-degree arc. Let AD=x. Then AC=x+20, because AC is the chord of a 2d-degree arc. In isosceles trapezoid ABCD, draw the altitude AF from A to BC, and notice that F divides BC into BF=11−2x​ and CF=11+2x​. Because the right triangles AFC2​ and AFB share the leg AF, it follows that
(x+20)2−(11+2x​)2=222−(11−2x​)2
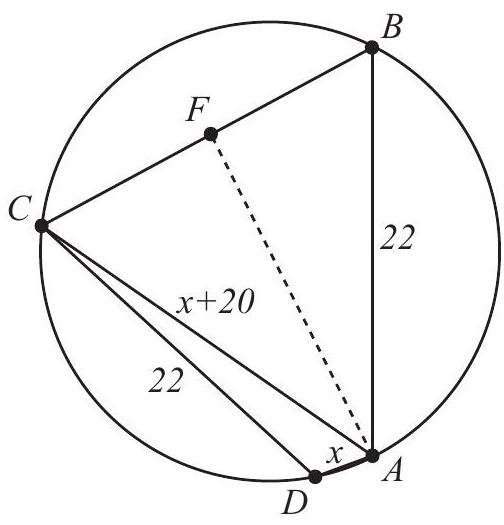
which simplifies to x2+18x−84=0. Thus x=−9+165​ and m+n=174​.
OR
Noting that ABCD is a cyclic isosceles trapezoid, apply Ptolemy's Theorem to obtain AB⋅BD=BC⋅AD+CD⋅AB, or (x+20)2=22x+222. Solve the equation to find that x=−9+165​.
Query: If the restriction d<120 were removed, then the problem would have an additional solution. Can you find it?
