Problem:
Find the area of the region enclosed by the graph of .
Solution:
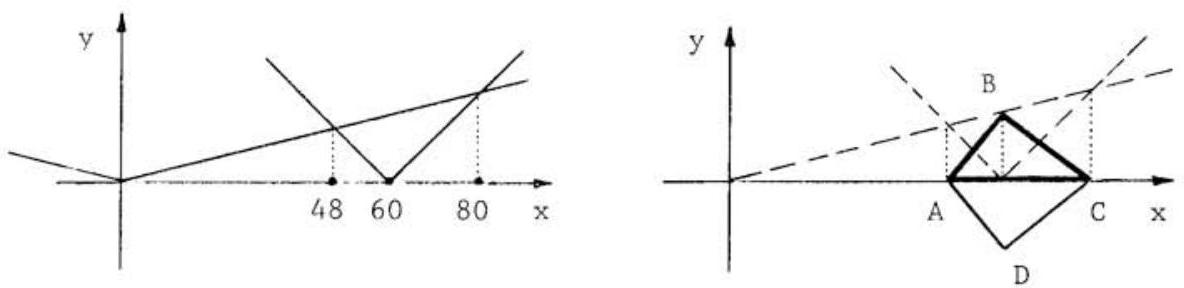
First we note that the graph of the given equation is symmetric with respect to the -axis, since the replacement of by does not change the equation. Consequently, it suffices to assume that , find the area enclosed above the -axis, and then double this area to find the answer to the problem.
By sketching both and on the same graph, as shown in the first figure below, we note that only if the graph of lies above that of . This occurs only between (where ) and (where . In this interval, the graph of with the -axis forms , as shown in the second figure. The base of this triangle is , its altitude (at ) is , hence its area is . Kite is the graph of ; the area enclosed by it is .
The problems on this page are the property of the MAA's American Mathematics Competitions