Problem:
An ellipse has foci at and in the -plane and is tangent to the -axis. What is the length of its major axis?
Solution:
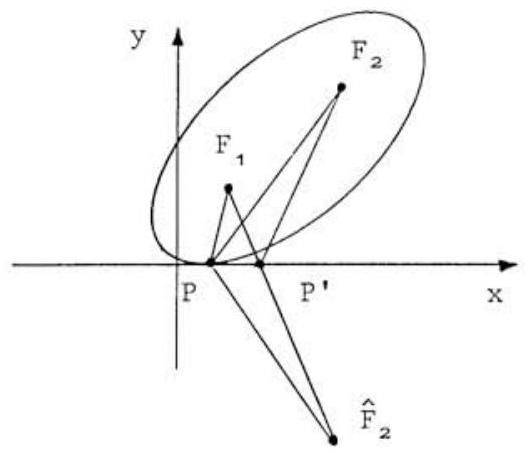
Let and denote the given foci, and , respectively, and let be the reflection of in the x-axis. We claim that , the length of the major axis of the ellipse, is equal to the length of the segment , which is easily found to be by the distance formula between two points in the plane.
To prove our claim, let be the point of tangency of the ellipse to the -axis, and assume that the segment intersects the -axis at the point , distinct from , as shown in the adjacent figure, where the location of the foci is purposefully distorted. Then, by the Triangle Inequality, one finds that
However, by the definition of the ellipse, for every point on the ellipse, . Hence, in particular,
Moreover, for every point outside the ellipse, one must have . Since, by the definition of tangency, must lie outside the ellipse, in particular it follows that
From and one may therefore conclude that
which is contrary to . This contradiction establishes the falsity of the assumption that and are distinct, and hence completes the proof of the claim.
The problems on this page are the property of the MAA's American Mathematics Competitions