Problem:
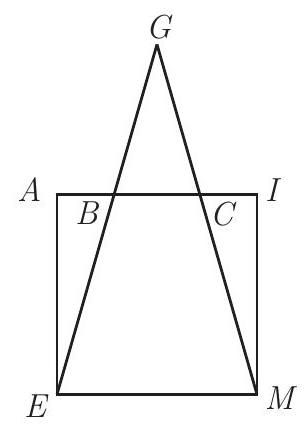
Square AIME has sides of length 10 units. Isosceles triangle GEM has base EM, and the area common to triangle GEM and square AIME is 80 square units. Find the length of the altitude to EM in △GEM.
Solution:
Let h be the required altitude, and let B and C be the points of intersection of AI with GE and GM, respectively. Then the fact that △GEM is similar to △GBC implies that hh−10=10BC. Thus BC=h10h−100, and the area common to GEM and AIME equals 21⋅10h−21(h10h−100)(h−10)=80. This equation reduces to 5h2−5(h−10)2=80h, or 100h−500=80h. The required length is then 25.
The problems on this page are the property of the MAA's American Mathematics Competitions