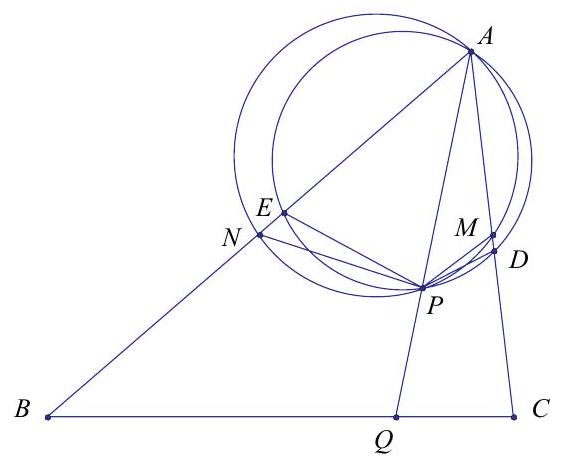
Problem:
In triangle ABC,AC=13,BC=14, and AB=15. Points M and D lie on AC with AM=MC and ∠ABD=∠DBC. Points N and E lie on AB with AN=NB and ∠ACE=∠ECB. Let P be the other point of intersection of the circumcircles of △AMN and △ADE. Ray AP meets BC at Q. The ratio CQBQ can be written in the form nm, where m and n are relatively prime positive integers. Find m−n.
Solution:
The Angle Bisector Theorem implies that E lies on AN and D lies on MC because AE/EB=AC/BC<1 and AD/DC=AB/CB>1. The Angle Bisector Theorem furthermore implies
NE=AN−AE=2AB−AC+BCAC⋅AB=185
and
MD=CM−CD=2AC−BC+BABC⋅AC=5813
Because ANPM is cyclic, ∠ENP=∠ANP=∠PMD. Because AEPD is cyclic, ∠NEP=180∘−∠AEP=∠ADP=∠MDP. Because ∠ENP= ∠PMD and ∠NEP=∠MDP, triangles NEP and MDP are similar. Hence
MDNE=MPNP
Applying the Law of Sines to △ANP and △AMP gives
MDNE=MPNP=sin∠PAMsin∠NAP=sin∠QACsin∠BAQ
and thus
sin∠QACsin∠BAQ=(5813)(185)=117145
Thus
QCBQ=Area(ACQ)Area(ABQ)=21⋅AC⋅AQ⋅sin∠QAC21⋅AB⋅AQ⋅sin∠BAQ=1315⋅117145=507725
and m−n=218.
The problems on this page are the property of the MAA's American Mathematics Competitions