Problem:
The diagram shows a rectangle that has been dissected into nine non-overlapping squares. Given that the width and the height of the rectangle are relatively prime positive integers, find the perimeter of the rectangle.
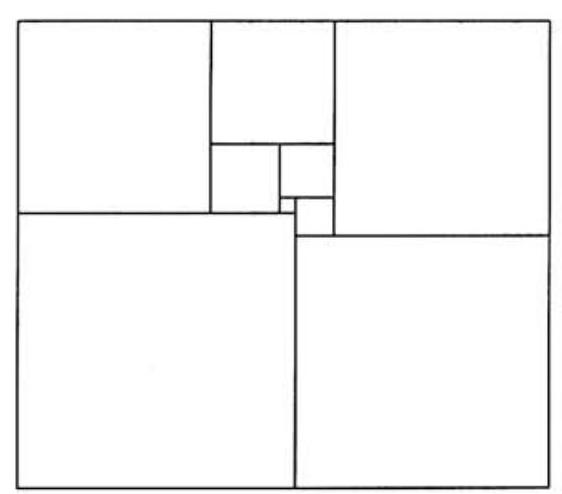
Solution:
Let and be the lengths of the sides of the two smallest squares, with . In the diagram below, each square has been labeled with the length of its sides.
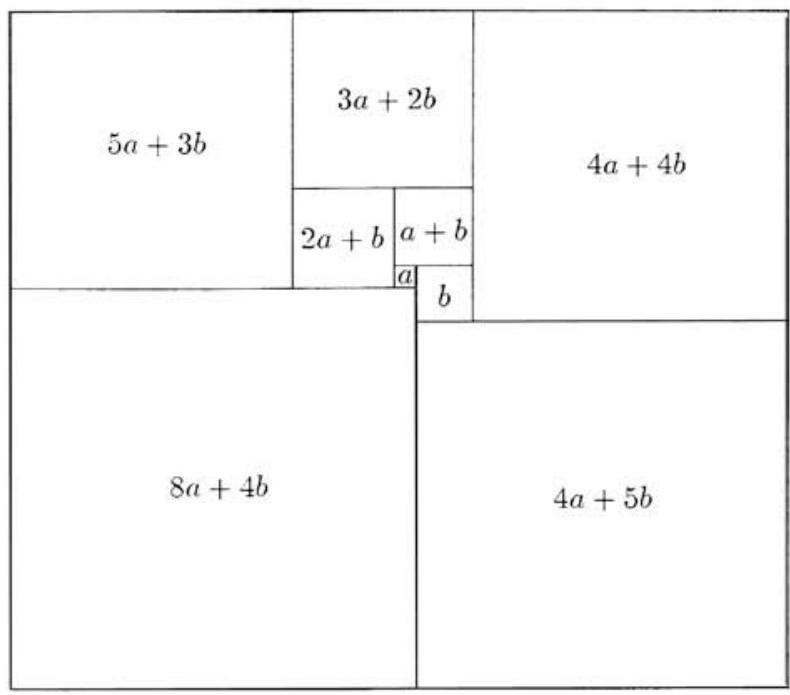
The length of the left side of the rectangle is equal to the length of the right side, so . This implies that there is a positive number for which and . Thus the width-to-height ratio for the rectangle is . Because the dimensions of the rectangle are relatively prime positive integers, they must be and . Therefore the perimeter is .
The problems on this page are the property of the MAA's American Mathematics Competitions