Problem:
Arnold is studying the prevalence of three health risk factors, denoted by , , and , within a population of men. For each of the three factors, the probability that a randomly selected man in the population has only this risk factor (and none of the others) is . For any two of the three factors, the probability that a randomly selected man has exactly these two risk factors (but not the third) is . The probability that a randomly selected man has all three risk factors, given that he has and is . The probability that a man has none of the three risk factors given that he does not have risk factor is , where and are relatively prime positive integers. Find .
Solution:
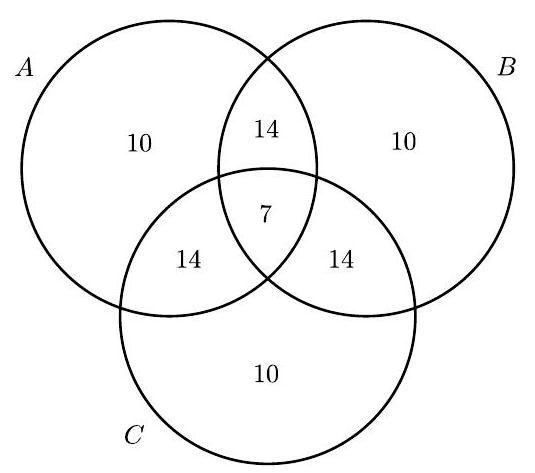
For simplicity, assume without loss of generality that the population is men, and sketch a Venn diagram displaying their risk factors. Each set showing the three risk factors by themselves must contain men, while each set showing the intersections of exactly two risk factors must contain men. To make the intersection of all three sets represent of the entire intersection of and , that intersection must contain men. Adding up all the numbers in the Venn diagram so far shows that the union of the three sets contains men. That leaves men who have none of the risk factors. Because there are men who do not have risk factor , the required probability is . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions