Problem:
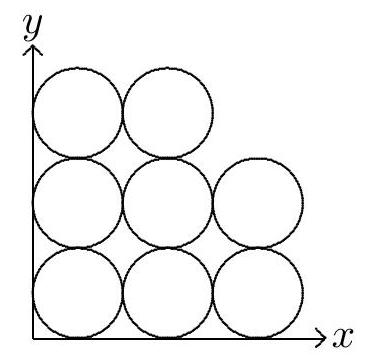
Eight circles of diameter are packed in the first quadrant of the coordinate plane as shown. Let region be the union of the eight circular regions. Line , with slope , divides into two regions of equal area. Line 's equation can be expressed in the form , where , and are positive integers whose greatest common divisor is . Find .
Solution:
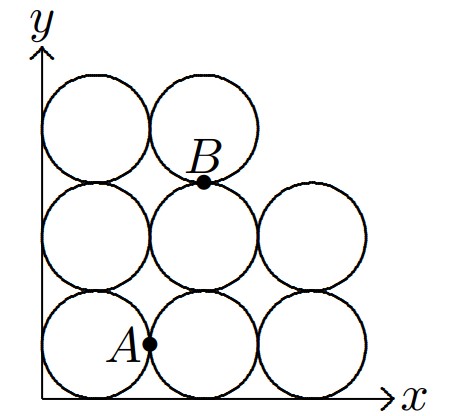
Such a line is unique. This is because when a line with equation intersects , then as decreases, the area of the part of above the line is strictly increasing and the area of the part of below the line is strictly decreasing. The symmetry point of the two circles that touch at is , and so any line passing through divides their region into two regions of equal area. Similarly, any line passing through divides the region consisting of the two circular regions that touch at into two regions of equal area. Of the remaining four circles, two of them are on either side of line . Thus line divides into two regions of equal area. Because the slope of line is , line is line , and it has equation or . Then .
The problems on this page are the property of the MAA's American Mathematics Competitions