Problem:
Jenny and Kenny are walking in the same direction, Kenny at feet per second and Jenny at foot per second, on parallel paths that are feet apart. A tall circular building feet in diameter is centered midway between the paths. At the instant when the building first blocks the line of sight between Jenny and Kenny, they are feet apart. Let be the amount of time, in seconds, before Jenny and Kenny can see each other again. If is written as a fraction in lowest terms, what is the sum of the numerator and denominator?
Solution:
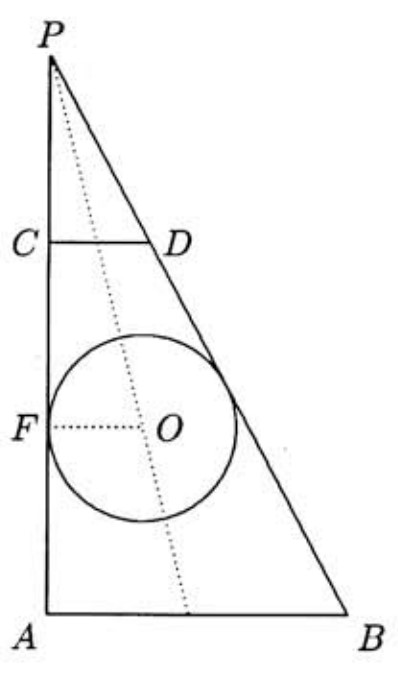
Let and , respectively, be Kenny's and Jenny's positions at the instant when the building first blocks their line of sight, and let and be their positions when they can first see each other again. Let be the point where extended meets extended. These two segments are tangent to the building and . Let be the center of the building, the point at which is tangent to the building, and the time in seconds that passes as Kenny walks from to . Then , , and . Since , we see that
so . Let be the measure of .
Since is the bisector of , it follows that has measure . Thus
Using
we compute
The sum of the numerator and denominator is .
Let Kenny walk to the right along the -axis, Jenny to the right along the line , and let the building be centered at . Then Kenny and Jenny lose sight of each other as they (simultaneously) cross the -axis. If we assume this happens at time , then at time , Kenny's position will be and Jenny's position will be . An equation for the line determined by Kenny's and Jenny's positions at time is
We wish to find the time when the distance from the center of the building to this line is . Using the formula for the distance from a point to a line, we have
which reduces to . This will be the case when or .
The problems on this page are the property of the MAA's American Mathematics Competitions