Problem:
The figure below shows a ring made of six small sections which you are to paint on a wall. You have four paint colors available and will paint each of the six sections a solid color. Find the number of ways you can choose to paint the sections if no two adjacent sections can be painted with the same color.
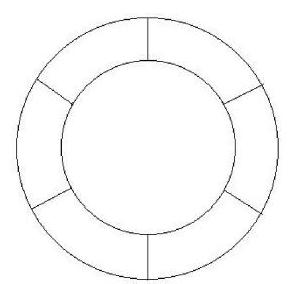
Solution:
Consider the problem of painting regions in a row rather than in a ring. Let be the number of ways to paint regions in a row so that no two adjacent regions receive the same color and the first and last regions are painted different colors. Let be the number of ways to paint the regions so that no two adjacent regions receive the same color and the first and last regions are painted the same color. Then and . Note that for and . Thus , and for , which allow the calculation of , and . The requested count is equal to . It is easy to verify that satisfies the required recursion.
The problems on this page are the property of the MAA's American Mathematics Competitions