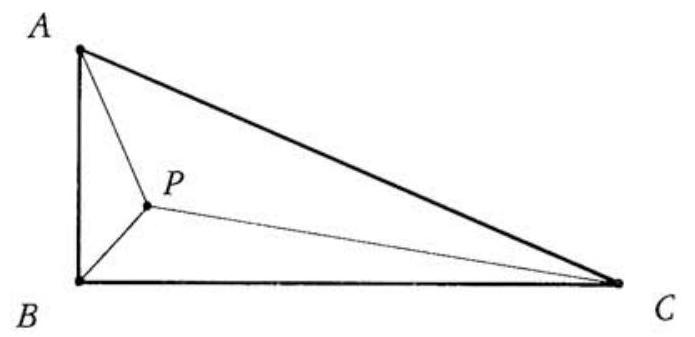
Problem:
Triangle ABC has right angle at B, and contains a point P for which PA=10,PB=6, and ∠APB=∠BPC=∠CPA. Find PC.
Solution:
Noting that ∠APB=∠BPC=∠CPA=120∘, and applying the Law of Cosines to △APB,△BPC and △CPA, we find that
(AB)2=(PA)2+(PB)2+PA⋅PB=100+36+60=196(1)
(BC)2=(PB)2+(PC)2+PB⋅PC=36+(PC)2+6PC(2)
and
(CA)2=(PC)2+(PA)2+PC⋅PA=(PC)2+100+10PC(3)
Since (AB)2+(BC)2=(CA)2 by the Pythagorean Theorem, it follows from (1), (2) and (3) that
196+[36+(PC)2+6PC]=(PC)2+100+10PC
from which PC=33.
The problems on this page are the property of the MAA's American Mathematics Competitions