Problem:
The vertices of △ABC are A=(0,0),B=(0,420), and C=(560,0). The six faces of a die are labeled with two A's, two B's, and two C's. Point P1=(k,m) is chosen in the interior of △ABC, and points P2,P3,P4,… are generated by rolling the die repeatedly and applying the rule: If the die shows label L, where L∈{A,B,C}, and Pn is the most recently obtained point, then Pn+1 is the midpoint of PnL. Given that P7=(14,92), what is k+m?
Solution:
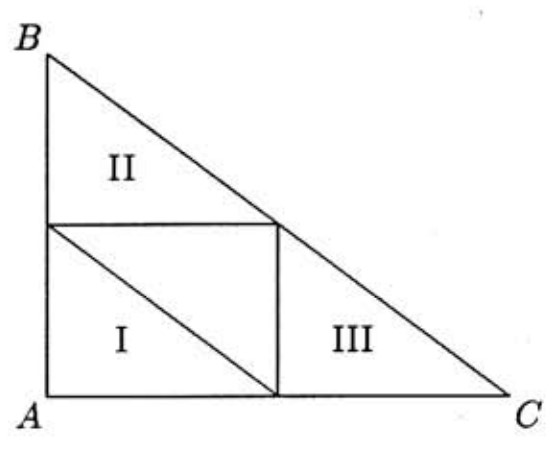
First note that, since P1 is inside △ABC, all subsequent points Pk will also be inside the triangle. Furthermore, as will be shown below, once any subsequent Pk is given, then P1 is uniquely determined. Suppose that Pk=(xk,yk) is known. Since Pk is inside △ABC, we have
0<xk<560,0<yk<420,0<420xk+560yk<420⋅560
If A is rolled, then
(xk+1,yk+1)=Pk+1=21Pk=(2xk,2yk),
so the range of possible positions of Pk+1 is limited to the original triangle contracted by a factor of 21 (region I in the diagram). Hence if A is rolled, then Pk+1 is in the interior of region I, and we may conclude that
420xk+1+560yk+1<21⋅420⋅560
Similarly, if B is rolled, then Pk+1 is in the interior of region II, so yk+1>210. If C is rolled, then Pk+1 is in the interior of region III, so xk+1>280. Thus, for k≥2,Pk must lie in one of the regions I,II,III, and its predecessor is uniquely determined. For example if Pk=(xk,yk) lies in region II, then Pk must be the midpoint of BPk−1. It follows that Pk−1=2Pk−B=(2xk,2yk−420). We can now construct a "predecessor function" as follows: if k≥2 and Pk=(xk,yk), then
Pk−1=⎩⎪⎪⎨⎪⎪⎧(2xk,2yk−420) if yk>210(2xk−560,2yk) if xk>280(2xk,2yk) if 420xk+560yk<21420⋅560
It is now easy to trace P7=(14,92) back to P1:
P7=(14,92)⟹P6=(28,184)⟹P5=(56,368)⟹P4=(112,316)⟹P3=(224,212)⟹P2=(448,4)⟹P1=(336,8).
We then see that k+m=336+8=344.
The problems on this page are the property of the MAA's American Mathematics Competitions