Problem:
Three circles, each of radius , are drawn with centers at and . A line passing through is such that the total area of the parts of the three circles to one side of the line is equal to the total area of the parts of the three circles to the other side of it. What is the absolute value of the slope of this line?
Solution:
First observe that the three circles are disjoint, i.e. their centers are more than units apart. Next note that any line through ) will divide the area of the circle centered there evenly. Thus the problem reduces to finding the value of for which the line given by
also divides the areas of the other two circles in the desired manner. To this end, note that such a line must pass exactly as far to the right of as it passes to the left of . Denoting this distance by , it follows that and must satisfy Equation , i.e.
from which and the answer to the problem is .
Note. As shown in the first figure below, in this case the uniqueness of the solution is assured by the fact that , the common length of the circles' radii. If the circles were positioned differently with respect to one another, or if the value of were larger than , as exemplified in the second figure below, then the resulting line would not necessarily yield a unique solution to the problem.
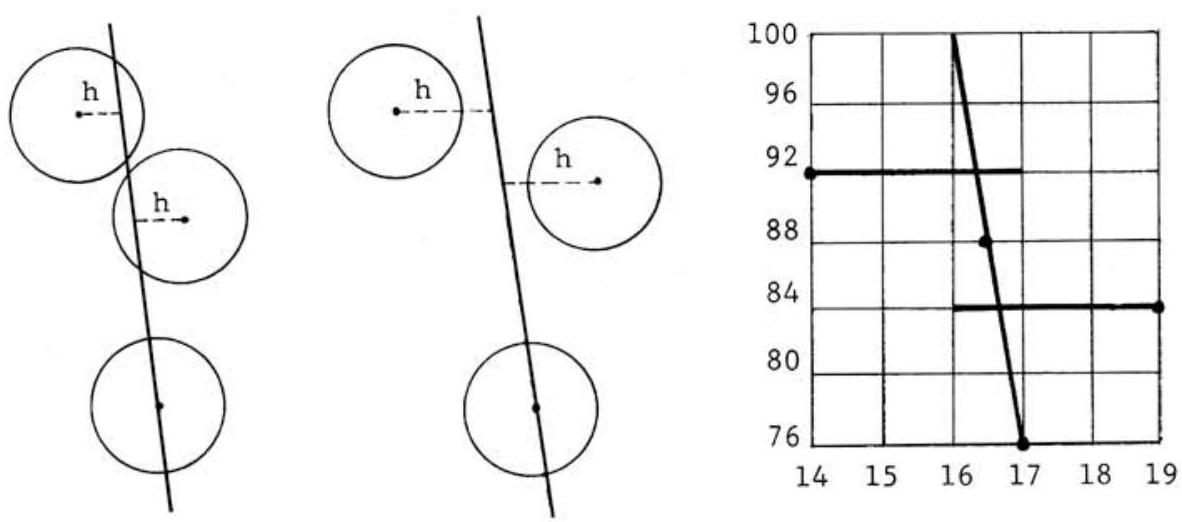
Note that the lines passing through , the center of symmetry of the two circles centered at and , divide the areas of these two circles in the manner desired. Consequently, the line through and , whose slope is , provides the answer to the problem. The uniqueness of the solution follows from observing that it intersects the radius from to of one circle and the radius from to of the other circle, as shown in the third figure above. (Note the difference in scales.)
The problems on this page are the property of the MAA's American Mathematics Competitions