Problem:
The graphs of the equations
are drawn in the coordinate plane for . These lines cut part of the plane into equilateral triangles of side . How many such triangles are formed?
Solution:
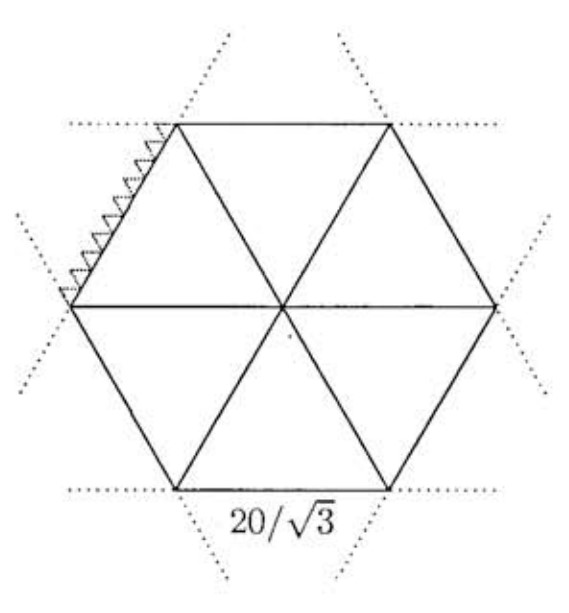
The six outermost lines determine a regular hexagon of side length . The three lines through the origin cut this hexagon into equilateral triangles, each with side length . Since each of these large triangles has side length times the side length of the small triangles, each of the large equilateral triangles is cut into small triangles. Hence the hexagon is cut into small triangles. In addition there is a row of ten triangles outside, but adjacent to, each side of the hexagon. (Some of these triangles are shown in the figure.) Therefore the total number of small triangles in the configuration is .
.jpg)
Let be a positive integer and consider the figure obtained by drawing the lines for . By symmetry, the number of equilateral triangles of side obtained is times the number that lie in the upper half plane in the wedge bounded by the lines and . Below the line there is triangle in the wedge. Between and there are triangles.
For , there are triangles between and , and in this row there are triangles oriented vertex-up and oriented vertex-down. Above the line there is a row of vertexup triangles, but because there is no horizontal line above , there are none that are vertex-down. Hence the number of equilateral triangles of side length is
When we have such triangles.
The problems on this page are the property of the MAA's American Mathematics Competitions