Problem:
A particle moves in the Cartesian plane from one lattice point to another according to the following rules:
From any lattice point , the particle may move only to , or .
There are no right angle turns in the particle's path. That is, the sequence of points visited contains neither a subsequence of the form ) nor a subsequence of the form .
How many different paths can the particle take from to ?
Solution:
Let be the number of permissible paths from to , and define . If or , then . If and , then the particle can reach from any of the points . Also, if the particle is at and next moves to , then the particle must have entered the row containing these points on a diagonal path, not a vertical one, because otherwise one of the moves to the right towards would make a right angle. Thus the number of ways to travel to in such a way that the path continuing to is permissible is
A similar statement holds for paths the particle can take to that result in a permissible path to . Thus,
This is simply the sum of the number of permissible paths from the origin to points on the top or right side of the rectangle with vertices . With this realization, calculate the number of permissible paths to each lattice point as shown in the grid below, to find that there are permissible paths.
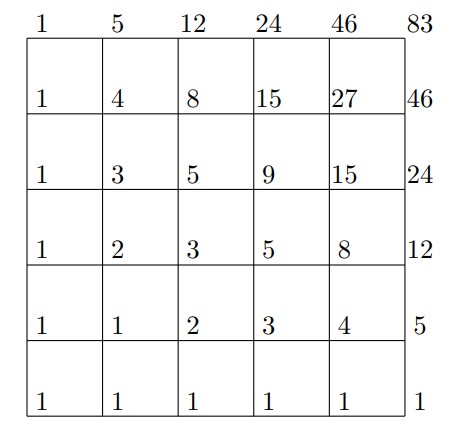
Label each vertex with an ordered triple whose first component represents the number of paths that end at that vertex with a diagonal step, whose second component represents the number of paths that end at that vertex with a step to the right, and whose third component represents the number of paths that end at that vertex with a step up. Begin by labeling the vertices with the triples , and as shown. For the other vertices, the first component at a vertex is the sum of the three components at the vertex diagonally below it and to the left, the second component at a vertex is the sum of the first two components at the vertex directly to its left, and the third component at a vertex is the sum of the first and third components at the vertex directly below it. Use these relationships to complete the labeling of the grid. The requested number of paths is the sum of the components in the upper right vertex, that is, .
.jpg)
The problems on this page are the property of the MAA's American Mathematics Competitions