Problem:
Two long cylindrical tubes of the same length but different diameters lie parallel to each other on a flat surface. The larger tube has radius and rolls along the surface toward the smaller tube, which has radius . It rolls over the smaller tube and continues rolling along the flat surface until it comes to rest on the same point of its circumference as it started, having made one complete revolution. If the smaller tube never moves, and the rolling occurs with no slipping, the larger tube ends up a distance from where it starts. The distance can be expressed in the form , where , and are integers and is not divisible by the square of any prime. Find .
Solution:
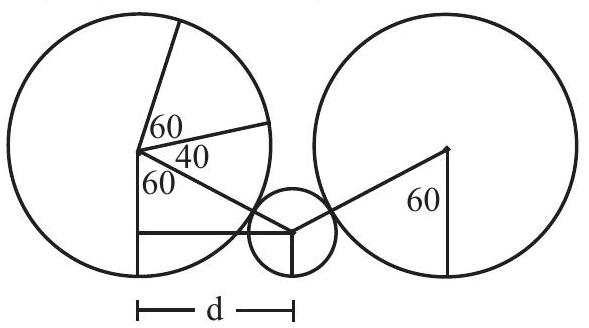
Let the larger tube roll until it is tangent to the smaller tube as shown in the diagram. At that point, the centers of the tubes are a horizontal distance apart, where is one leg of a right triangle with hypotenuse and other leg . It follows that the triangle is a triangle with a angle at the center of the smaller tube, is equal to , and the larger tube rests on a point of its circumference from the point of its circumference where it is tangent to the smaller tube. When the larger tube finishes rolling over the smaller tube, it is tangent to the smaller tube on the other side of the smaller tube. Its center has moved a horizontal distance of . It has rolled over an arc of of the smaller tube, and thus it has rolled over an arc of one-third of , or of the larger tube. The point of its circumference where the larger tube rests after rolling over the smaller tube is from the point where it rested before rolling over the smaller tube. Thus the larger tube has rolled over an arc of while moving horizontally a distance of . When the larger tube completes one revolution, it has rolled horizontally by rolling through of arc and moving a distance of . Therefore the total horizontal distance covered is . Thus .
The problems on this page are the property of the MAA's American Mathematics Competitions