Problem:
In tetrahedron , edge has length . The area of face is and the area of face is . These two faces meet each other at a angle. Find the volume of the tetrahedron in .
Solution:
Let be the volume of tetrahedron and the altitude of the tetrahedron corresponding to . Then , which will be determined upon finding .
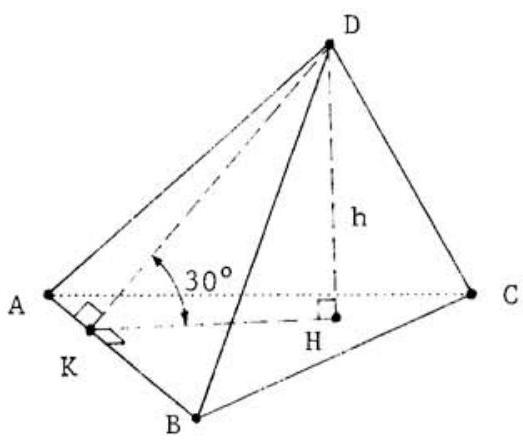
By definition, for the angle between faces and to be , planes perpendicular to must cut the two faces in rays which form a angle. Choose such a plane through , let be its intersection with , and let be the point on the line of intersection of the plane chosen and the plane of so that . These are shown in the adjoining figure.
Since , we find that .
Moreover, since is a triangle, it follows that . Consequently, substituting into the formula given in the first paragraph, we find that .
The problems on this page are the property of the MAA's American Mathematics Competitions