Problem:
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as , where and are positive integers. Find .
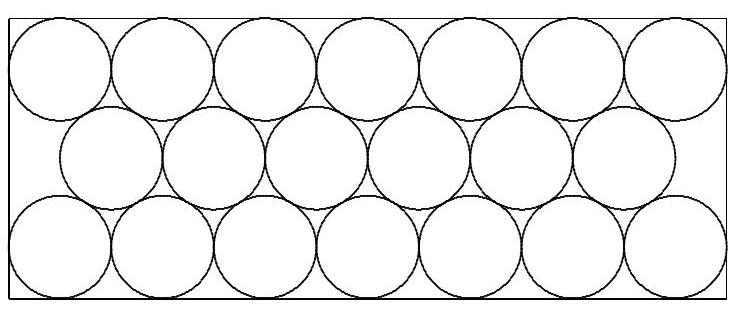
Solution:
Let be the radius of each circle, and let and be the dimensions of the rectangle with . Then . Now consider the equilateral triangle whose vertices are the centers of any three mutually tangent circles. The height of such a triangle is , so . It follows that
so .
The problems on this page are the property of the MAA's American Mathematics Competitions