Problem:
Let T be the set of ordered triples (x,y,z) of nonnegative real numbers that lie in the plane x+y+z=1. Let us say that (x,y,z) supports (a,b,c) when exactly two of the following are true: x≥a,y≥b,z≥c. Let S consist of those triples in T that support (21,31,61). The area of S divided by the area of T is m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
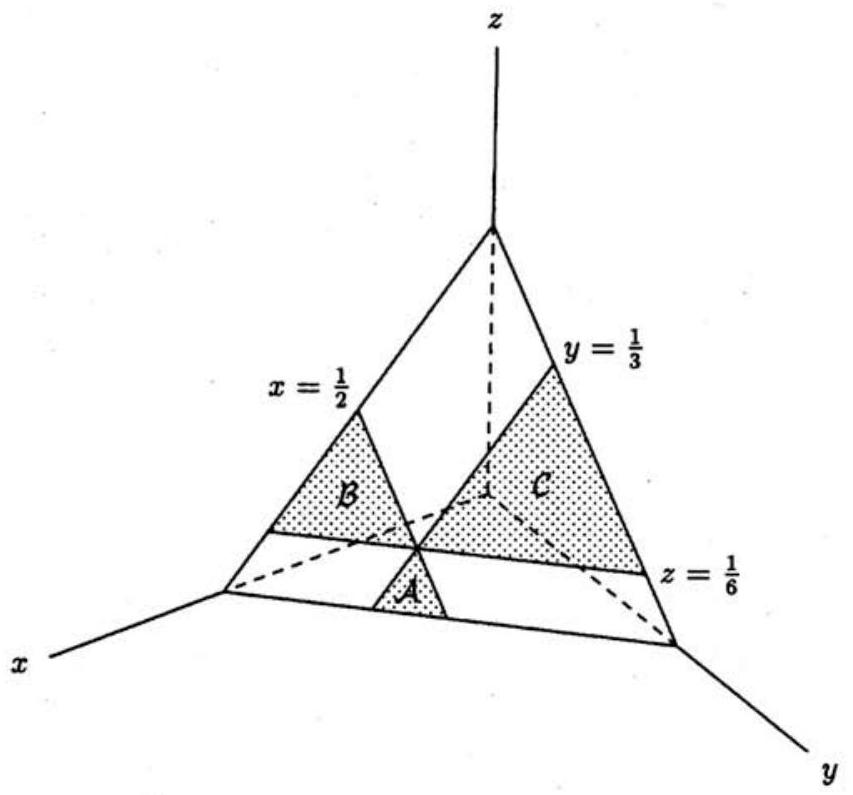
Notice that T is a first-octant equilateral triangle, whose vertices are (1,0,0),(0,1,0), and (0,0,1). The planes x=21,y=31, and z=61 intersect T along line segments that are parallel to the sides of T. Let A consist of those points of T that satisfy x≥21 and y≥31. Notice that z≤61 for any point in A, so the points of A support (21,31,61), with the exception of (21,31,61) itself. In a similar fashion, let B consist of those points of T that satisfy x≥21 and z≥61, and let C consist of those points of T that satisfy y≥31 and z≥61. Except for the point (21,31,61),S is the union of the equilateral triangles A,B, and C, whose sides are 61,31, and 21 times as long as the sides of T, and whose areas are 361,91, and 41 times the area of T, respectively. It follows that the area of S divided by the area of T is 361+91+41=187. Thus m+n=25.
The problems on this page are the property of the MAA's American Mathematics Competitions
