Problem:
A square piece of paper has sides of length . From each corner a wedge is cut in the following manner: at each corner, the two cuts for the wedge each start at distance from the corner, and they meet on the diagonal at an angle of (see the figure below). The paper is then folded up along the lines joining the vertices of adjacent cuts. When the two edges of a cut meet, they are taped together. The result is a paper tray whose sides are not at right angles to the base. The height of the tray, that is, the perpendicular distance between the plane of the base and the plane formed by the upper edges, can be written in the form , where and are positive integers, , and is not divisible by the th power of any prime. Find .
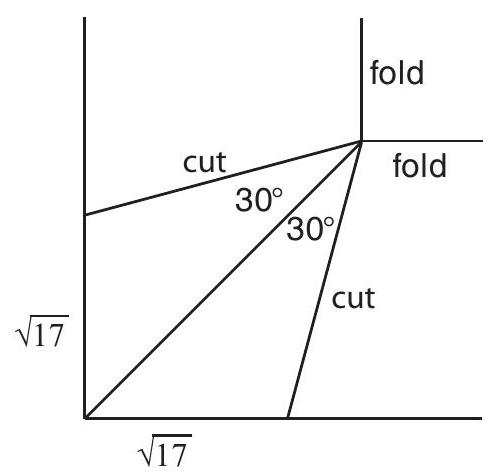
Solution:
Place the paper in the Cartesian plane with a corner at the origin and two of the sides on the positive coordinate axes. Label the origin as . Let be the point on the -axis from which the cut starts, be the point of intersection of the two cuts made near this corner, the foot of the perpendicular from to the -axis, the foot of the perpendicular from to , and the point of intersection of and (see the accompanying figure).
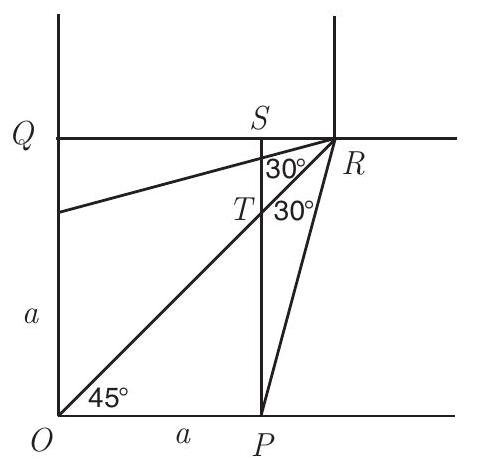
Let . When the left and bottom edges of the paper are folded up to create two sides of the tray, the cut edges will meet, by symmetry, above the line , that is, above segment . As the bottom edge folds up, point traces a circular arc, with the arc centered at and of radius . When the cut edges of the two sides meet, will be at the point directly above . Because is perpendicular to the -plane, is the height of the tray.
Observe that . Applying the Law of Sines in yields
Then in right triangle ,
It then follows that
Next apply the Pythagorean Theorem to right triangle to find that
so . Hence the height of the tray is , and so .
The problems on this page are the property of the MAA's American Mathematics Competitions