Problem:
A triangular array of squares has one square in the first row, two in the second, and, in general, squares in the th row for . With the exception of the bottom row, each square rests on two squares in the row immediately below, as illustrated in the figure. In each square of the eleventh row, a or a is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of 's and 's in the bottom row is the number in the top square a multiple of ?
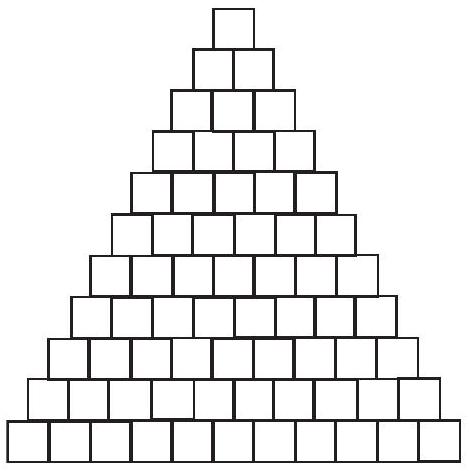
Solution:
Number the rows from bottom to top, with the bottom row numbered and the top row numbered . Let the entries in row , from left to right, be , where each is or . In row (the th row from the bottom) label the squares from left to right by . It can then be shown by induction that the number in row and square , is
Thus the entry in the top square (in row ) is
It is easy to check that is a multiple of for . Thus
For this last expression to be a multiple of , either or three of these four numbers are and the fourth is . Thus there are five choices of that make the sum a multiple of . Furthermore, each of can be either or , so these values can be assigned in ways. Thus there are initial distributions that result in the number in the top square being a multiple of .
The problems on this page are the property of the MAA's American Mathematics Competitions