Problem:
Let and be the endpoints of a semicircular arc of radius . The arc is divided into seven congruent arcs by six equally spaced points , . All chords of the form or are drawn. Let be the product of the lengths of these twelve chords. Find the remainder when is divided by .
Solution:
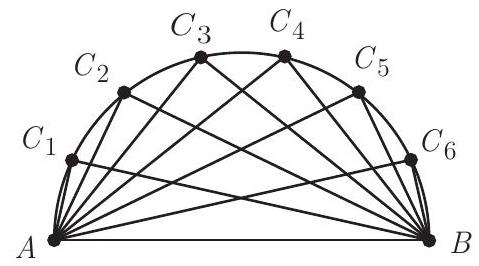
Draw the semicircular arc in the complex plane so that is at and is at . This arc is then half the circle of radius centered at 0 and the twelve given chords are congruent to the twelve chords , , where are the reflections of in the real axis. The points are then the fourteenth roots of , all satisfying the equation . The chord from point to has the same length as the modulus of the complex number . These complex numbers each satisfy the equation . The product of the lengths of the original twelve chords and is the same as the modulus of the product of the roots of the equation . The product of the roots is equal to the constant term in the fraction when written as a polynomial. According to the Binomial Theorem, this constant term is . This product equals the required product times , which equals , so is , and the requested remainder is .
The problems on this page are the property of the MAA's American Mathematics Competitions