Problem:
A semicircle with diameter is contained in a square whose sides have length . Given that the maximum value of is , where and are integers, find .
Solution:
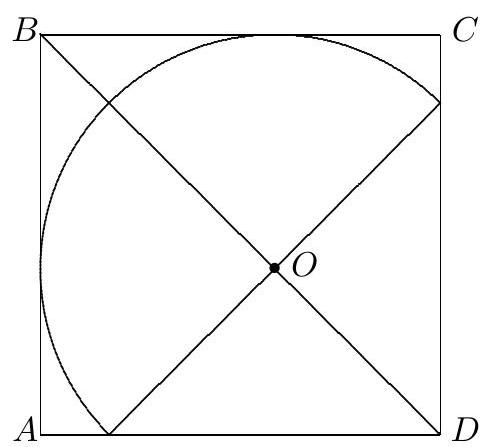
Any semicircle that is contained in a square can be translated to yield a semicircle that is inside the square and tangent to two adjacent sides of the square. Name the square , and, without loss of generality, consider semicircles tangent to and . The center of any such semicircle is equidistant from and and therefore must lie on diagonal . Let be the circle determined by the semicircle. The placement of that yields the largest semicircle is the point at which the intersection of with the square region is a semicircle. This is because if were placed closer to , the radius of would be smaller; and if were placed farther from , the intersection of and the square region would be an arc of less than , and so no semicircle centered at would fit in the square. Because is a symmetry line for the desired semicircle and the square, is the perpendicular bisector of the diameter joining the endpoints of the semicircle.
Let the radius of the largest semicircle be . Then the distance from to is . The sum of the distances from to and is , so the diameter of the largest semicircle that fits in the square is . Thus .
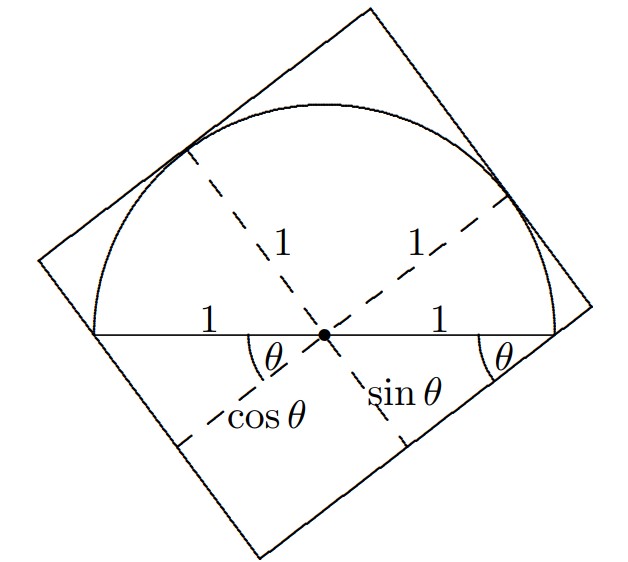
Consider a related problem: find the least possible side-length of a square that contains a semicircle for which the diameter is fixed. Let the orientation of the square with respect to the semicircle be such that the sides of the square and the diameter of the semicircle determine angles of and , with . Without loss of generality, assume the radius of the semicircle is . The opposite sides of the square are parallel, and, in general, if a pair of parallel lines touch a semicircle, then one will be tangent to its arc and one will contain an endpoint of the diameter. The diagram shows two perpendicular pairs of parallel lines with all four lines touching the semicircle. The distance between the lines in each pair is as small as possible because each line of the pair touches the semicircle. Thus the greater of these two distances is the minimal side-length of a square in this orientation that contains the semicircle. Because the distances between the pairs of parallel lines are and , the minimal side-length of a square in this orientation that contains the semicircle is . For between and , this length is minimum when , so the minimum length for any orientation of the square is . To find the maximum value of , solve the proportion to obtain . Thus .
The problems on this page are the property of the MAA's American Mathematics Competitions