Problem:
Square is . For , the lengths of the sides of square are half the lengths of the sides of square , two adjacent sides of square are perpendicular bisectors of two adjacent sides of square , and the other two sides of square are the perpendicular bisectors of two adjacent sides of square . The total area enclosed by at least one of can be written in the form , where and are relatively prime positive integers. Find .
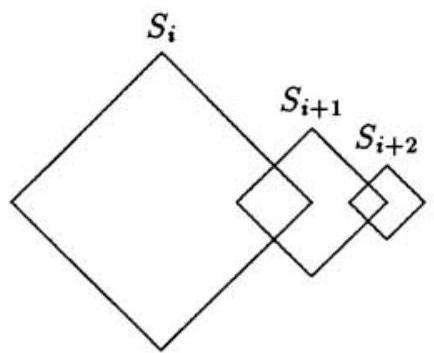
Solution:
Observe that the area of is one fourth that of , and that three fourths of is not inside . Therefore the area enclosed by at least one of is
Hence .
The problems on this page are the property of the MAA's American Mathematics Competitions