Problem:
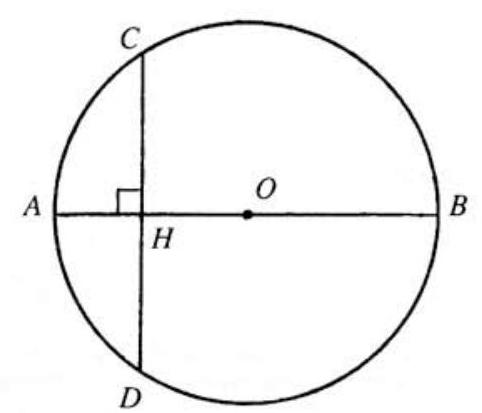
Diameter of a circle has length a -digit integer (base ten). Reversing the digits gives the length of the perpendicular chord . The distance from their intersection point to the center is a positive rational number. Determine the length of .
Solution:
Let , where and are digits. Then . We must now find and for which will be a positive rational. Evidently, ; to insure that is positive we take .
Since is a right triangle, we may use the Pythagorean Theorem to express in terms of and :
It follow's that is rational iff is rational. But the square root of an integer is rational only if it is integral. Thus, we must find and for which is a perfect square, and this will be the case only if there is a positive integer such that
Now cannot divide . (Why?) Therefore, it must divide . But this is possible only if is . (Why?) It follows that . Thus, we seek two numbers whose sum is and whose difference is a perfect square.
Finally, we examine all and for which : and . Only in the last case is a perfect square. Thus .
.jpg)
The problems on this page are the property of the MAA's American Mathematics Competitions