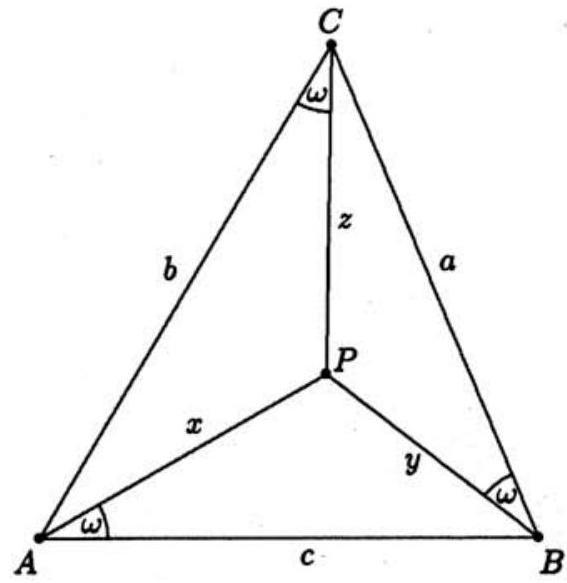
Problem:
Point P is located inside triangle ABC so that angles PAB,PBC, and PCA are all congruent. The sides of the triangle have lengths AB=13,BC=14, and CA=15, and the tangent of angle PAB is m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let ω denote the common measure of angles PAB,PBC, and PCA; let a,b, and c denote BC,CA, and AB; and let x,y, and z denote PA,PB, and PC. Apply the Law of Cosines to triangles PCA,PAB, and PBC to obtain
x2=z2+b2−2bzcosωy2=x2+c2−2cxcosωz2=y2+a2−2aycosω
Sum these three equations to obtain 2(cx+ay+bz)cosω=a2+b2+c2. Because the combined area of triangles PAB,PBC, and PCA is 21(cx+ay+bz)sinω, the preceding equation can be rewritten as
tanω=a2+b2+c24[ABC]
where [ABC] denotes the area of triangle ABC. With a=14,b=15, and c=13, use Heron's formula to find that [ABC]=84. It follows that tanω=168/295, so m+n=463.
Query: Triangle ABC has two Brocard points, and P is one of them. The other one is the point Q for which angles QBA,QCB, and QAC are equal. What is the common measure of these three angles?
The problems on this page are the property of the MAA's American Mathematics Competitions