Problem:
Find the number of positive integers whose value can be uniquely determined when the values of , , and are given, where denotes the greatest integer less than or equal to the real number .
Solution:
Call an integer good if it is uniquely determined by the values of , and . If is good, then the ordered triples and are not identical, so they must differ in at least one coordinate. This implies that is a multiple of 4 , 5 , or 6. Similarly, and are not identical, so is a multiple of 4 , 5 , or 6 . Because it is impossible for both and to be even, one of these must be a multiple of 5 . These conditions are both necessary and sufficient.
Assume first that is a multiple of 5 and is a multiple of 4 or 6 or both. Then and is congruent to -1 modulo either 4 or 6 , implying that is , or 11 modulo 12 . In this case, the Chinese Remainder Theorem implies that there are 4 good values of from 1 through . They are , and 55 .
Next assume that is a multiple of 5 and is a multiple of 4 or 6 or both. Then and , 6 , or , and again there are 4 good values of from 1 through 60 . They are , and 54 .
Hence there are good integers from 1 through 60 , so there are good positive integers less than or equal to 600 .
OR
As in the first solution, use the term good to refer to an integer that can be uniquely determined from the given values. Fix a positive integer between 1 and . The set of integers such that is an interval of four consecutive integers, where the least of these integers is divisible by 4. Similarly, the set of integers such that is an interval of five consecutive integers, where the least is divisible by 5 ; and the set of integers such that is an interval of six consecutive integers, where the least is divisible by 6 . Under this reformulation of the problem, is good if and only if these three intervals intersect in exactly one point.
There are two key observations about such intervals. First, these three intervals are guaranteed to have nonempty intersection because lies in all three intervals. Second, the intervals of lengths 4 and 6 must intersect in an interval of even length because the leftmost numbers in both intervals have the same parity. From these two observations, all relative positions of the three intervals can be determined. Indeed, fixing the position of the interval of length 6 , there are 4 locations for the interval of length 4 ; then, by the even length condition, there are 2 ways to place the interval of length 5 so that all three intervals intersect at a single point. Thus there are ways to position the intervals relative to each other to obtain the desired condition. These eight configurations are displayed below.
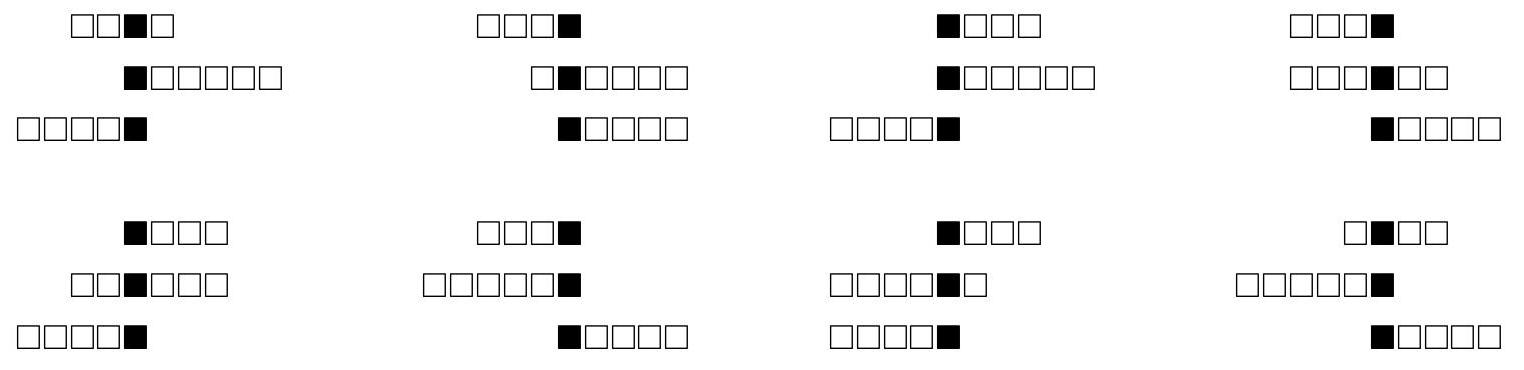
Finally, by the Chinese Remainder Theorem, for every integer , each configuration above can be achieved by exactly one integer in . This means that 8 values in the set are good, so values in the set are good.
The problems on this page are the property of the MAA's American Mathematics Competitions