Problem:
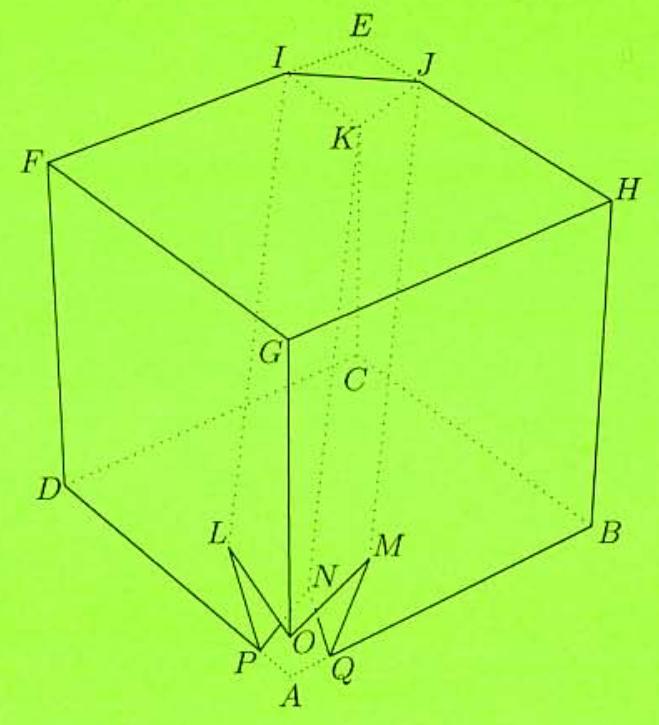
Let , and be three adjacent square faces of a cube, for which , and let be the eighth vertex of the cube. Let , and be points on , , and , respectively, so that . A solid is obtained by drilling a tunnel through the cube. The sides of the tunnel are planes parallel to , and containing the edges , and . The surface area of . including the walls of the tunnel, is , where , and are positive integers and is not divisible by the square of any prime. Find .
Solution:
Assign coordinates , , and . The line through that is parallel to can be described by , so this line meets the cube again when , at . By symmetry, the lines through and that are parallel to intersect the cube again at and , respectively. It is straightforward to show that the plane determined by , and is described by the equation , so that the plane meets the -axis at . By symmetry, the tunnel intersects the -axis at and the -axis at . As the diagram shows, one end of the tunnel has a triangular opening , while the other has a non-planar hexagonal opening . The surface of consists of nine polygonal faces, three of each of three types. It is straightforward to show that the area of pentagon IFGHJ and the area of hexagon are both . To find the area of pentagon , first obtain , , and . Then calculate the area of rectangle to be and the area of isosceles triangle to be . Thus the total surface area of is , and .
The problems on this page are the property of the MAA's American Mathematics Competitions