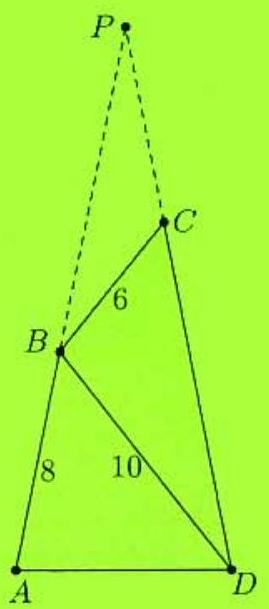
Problem:
In quadrilateral ABCD,∠BAD≅∠ADC and ∠ABD≅∠BCD,AB=8,BD=10, and BC=6. The length CD may be written in the form m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let P be the point where AB and DC intersect when extended. Since angles PCB and PBD are supplements of angles BCD and ABD, respectively, angles PCB and PBD are congruent, which implies that triangles PCB and PBD are similar. Now
PDPD−8=PDPB=BDCB=106
so PA=PD=20 and PB=12. Then 12PC=106, so PC=7.2 and CD=12.8=64/5. Thus m+n=69.
Query: Can you prove that B is between A and P and that C is between D and P ?
The problems on this page are the property of the MAA's American Mathematics Competitions