Problem:
A beam of light strikes at point with angle of incidence and reflects with an equal angle of reflection as shown. The light beam continues its path, reflecting off line segments and according to the rule: angle of incidence equals angle of reflection. Given that and , determine the number of times the light beam will bounce off the two line segments. Include the first reflection at in your count.
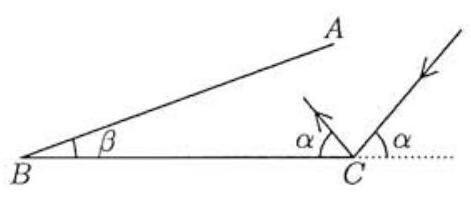
Solution:
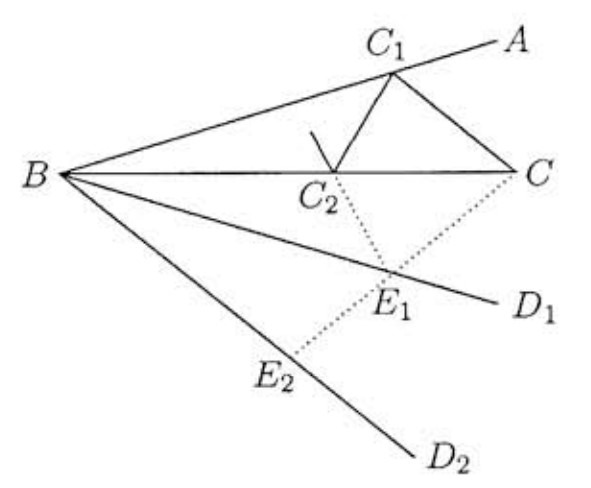
Label the points at which the light reflects as as shown. Draw so that and . Now reflect the path of the light inside across , and let be the reflection of . For counting purposes, it doesn't matter whether we look at the real path or the reflected path beginning with , so assume that the light beam actually begins its path by travelling from to . Now draw with and . Reflect the new path of the light beam across and let the reflection of be . Since , the path must be a straight line.
Repeat the above process by constructing with and . The result is a new path which follows the ray . Each point where the light beam reflects off or will correspond to an intersection point of this ray with some . We need to count these intersections. Draw the circle with center and radius as shown. The path that concerns us is the line segment where is on the circle and . (Once the ray leaves the circle, there will be no more reflections in the original path since the light beam will be outside .) To count the number of intersections first find . Since , we have , so . Hence the number of intersections equals
where is the greatest integer less than or equal to , and we add to count the first reflection at . With and , we obtain reflections.
.jpg)
The problems on this page are the property of the MAA's American Mathematics Competitions