Problem:
Let be the graph of , and denote by the reflection of in the line . Let the equation of be written in the form
Find the product .
Solution:
Let be any point on , and let be the corresponding point on , that is, the reflection of in the line . Connect and by a straight line segment as shown in the figure. Then the problem is to find an equation relating and .
Since is perpendicular to the line , its slope is . Thus
Furthermore, since the midpoint of is on the line , its coordinates must satisfy the equation of this line; that is,
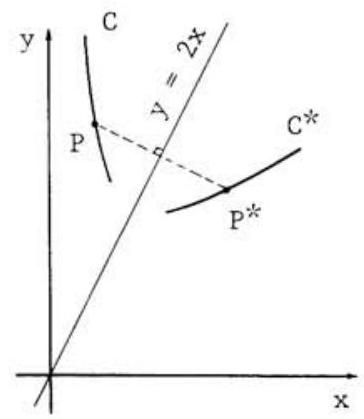
Solving and simultaneously for and yields and . Substituting these into (which holds since is on ) we find that
This is the equation of in the form desired; in it .
The problems on this page are the property of the MAA's American Mathematics Competitions