Problem:
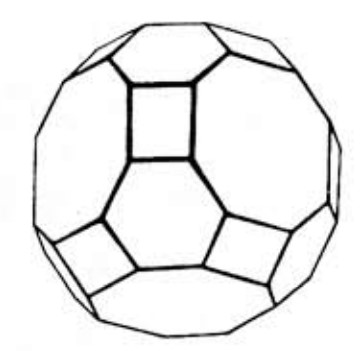
A convex polyhedron has for its faces squares, regular hexagons, and regular octagons. At each vertex of the polyhedron one square, one hexagon, and one octagon meet. How many segments joining vertices of the polyhedron lie in the interior of the polyhedron rather than along an edge or a face?
Solution:
Let and denote the number of vertices, edges, facial diagonals and interior diagonals of the polyhedron. We will evaluate them in succession, starting with .
Since at each vertex of the polyhedron there is exactly one of each kind of face, and since the vertices of each of the square faces must be at different vertices of the polyhedron,
(Note that the same value results if we consider the hexagonal or octagonal faces.)
Since there are edges emanating from each vertex of the polyhedron, and since counts each edge twice,
To find , note that each square face has diagonals, each hexagonal face has diagonals, and each octagonal face has diagonals. Consequently
Finally, because the polyhedron is convex, we may find by subtracting the number of edges and the number of facial diagonals from the total number of ways to connect pairs of vertices for the polyhedron. Thus
Note: The polyhedron in question is the "great rhombicuboctahedron", also known as the (rhombi)truncated cuboctahedron. It is one of the thirteen semi-regular (Archimedean) solids.
The problems on this page are the property of the MAA's American Mathematics Competitions