Problem:
Twelve congruent disks are placed on a circle of radius in such a way that the twelve disks cover , no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure to the right. The sum of the areas of the twelve disks can be written in the form , where are positive integers and is not divisible by the square of any prime. Find .
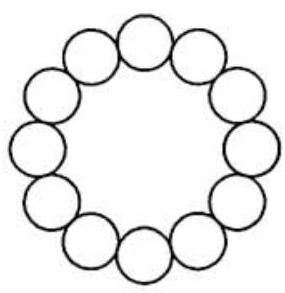
Solution:
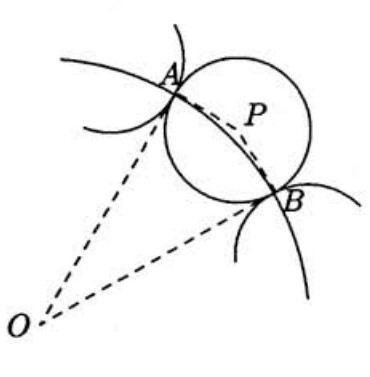
Since the disks cover and each of the disks is tangent to its two neighbors, must pass through the points of tangency. The accompanying figure shows one of the covering disks, arcs of the two adjacent disks, and part of . Let and be the points of tangency. By symmetry, the lines mutually tangent to adjacent disks must all pass through the center, , of . Let be the center of the disk shown. Then is a right angle, and . Thus the radius of each of the twelve disks is
Hence each of the disks has area . The sum of the areas of the twelve disks is
and we have .
The problems on this page are the property of the MAA's American Mathematics Competitions