Problem:
A car travels due east at mile per minute on a long, straight road. At the same time, a circular storm, whose radius is miles, moves southeast at mile per minute. At time , the center of the storm is miles due north of the car. At time minutes, the car enters the storm circle, and at time minutes, the car leaves the storm circle. Find .
Solution:
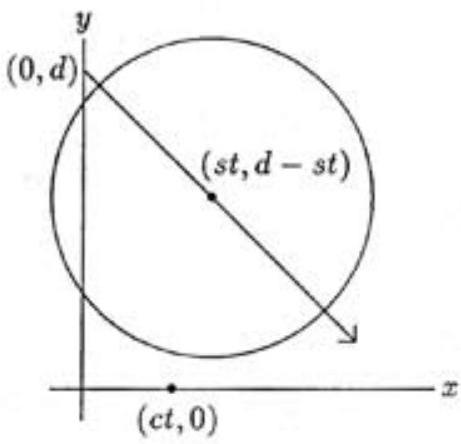
Let be the radius of the storm, be the distance from the center of the storm to the car at time be the speed of the car, and be the speed of the storm. Set up a coordinate system so that, at , the storm center is at , and the car is at the origin, moving along the positive -axis. At any time , the car is at and the storm center is at . When the car is entering or leaving the storm circle, the distance between these two points is . In other words, and are the solutions to
which can be rewritten as . The sum of the two roots of this quadratic equation is
Now use the given data , and to find that
The discriminant of the quadratic equation is nonnegative in this case, therefore and are real. The answer is otherwise independent of .
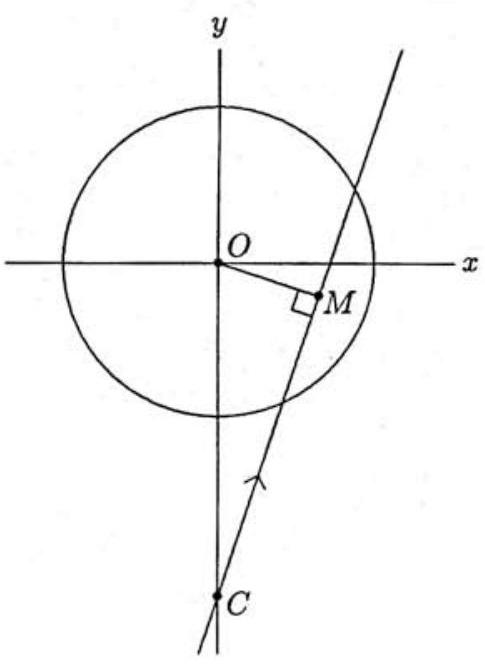
Make the storm center the origin of a coordinate system that has its positive -axis pointing east. At time , the car is at . Each minute thereafter, its position relative to the storm center is shifted by the velocity vector
due to the combined motion of the car and storm, respectively. The resulting linear path of the car intersects the storm along a chord of the circle, whose midpoint is reached at time . Because angle is right, and is , it follows that . To find the time it takes for the car to reach , divide this distance by the relative speed of the car, which is . It follows that
The problems on this page are the property of the MAA's American Mathematics Competitions