Problem:
A given sequence of distinct real numbers can be put in ascending order by means of one or more "bubble passes". A bubble pass through a given sequence consists of comparing the second term with the first term and exchanging them if and only if the second term is smaller, then comparing the third term with the current second term and exchanging them if and only if the third term is smaller, and so on in order, through comparing the last term, , with its current predecessor and exchanging them if and only if the last term is smaller.
The example below shows how the sequence is transformed into the sequence by one bubble pass. The numbers compared at each step are underlined.
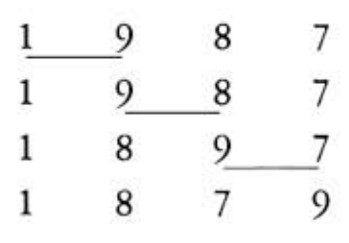
Suppose that , and that the terms of the initial sequence are distinct from one another and are in random order. Let , in lowest terms, be the probability that the number that begins as will end up, after one bubble pass, in the place (i. e., will have terms on its left and terms on its right). Find .
Solution:
The key property of bubble pass is that immediately after is compared with its predecessor and possibly switched, the current is the largest member of the set . Also, this set is the same at this point as it was originally, though the order of its elements in the sequence may be very different. These assertions can be verified by induction.
For a number m, which is initially before in the sequence, to end up as , two things must happen: must move into the position when the current and are compared, and it must not move out of that position when compared to . Therefore, by the key property, must be the largest number in the original , but not the largest in the original . In other words, of the first numbers originally, the largest must be and the second largest must be , which in our case is .
Whatever the first numbers are, there are equally likely orderings of them. Of these, : have the largest of them in the st slot and the second largest in the th slot. (The other numbers have : equally likely orderings.) Thus the desired probability must be , and hence .
The problems on this page are the property of the MAA's American Mathematics Competitions