Problem:
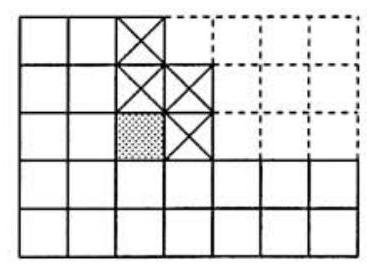
In a game of Chomp, two players alternately take "bites" from a -by- grid of unit squares. To take a bite, the player chooses one of the remaining squares, then removes ("eats") all squares found in the quadrant defined by the left edge (extended upward) and the lower edge (extended rightward) of the chosen square. For example, the bite determined by the shaded square in the diagram would remove the shaded square and the four squares marked by . (The squares with two or more dotted edges have been removed from the original board in previous moves.) The object of the game is to make one's opponent take the last bite. The diagram shows one of the many subsets of the set of unit squares that can occur during games of Chomp. How many different subsets are there in all? Include the full board and the empty board in your count.
Solution:
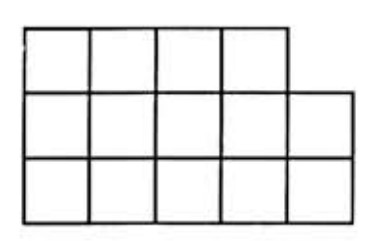
At any stage of the game, the uneaten squares will form columns of non-increasing heights as we read from left to right. It is not hard to show that this condition is not only necessary, but is also sufficient for a given configuration of squares to occur in a game. (The reader should prove this fact.) Moreover, any such configuration can be completely described by the twelvestep polygonal path that runs from the upper left to the lower right of the original board, forming the boundary between the eaten and uneaten squares. This polygonal boundary can be described by a twelve-letter sequence of 's and 's. Such a sequence contains seven 's, where each represents the top of an uneaten column (or the bottom of a completely eaten one) and five 's, where each represents a one-unit drop in vertical height in moving from the top of an uneaten column to the top of an adjacent, but shorter column. For example, the state that appears in the diagram accompanying the problem is described by , while the state in the diagram above is given by . There are sequences of seven 's and five 's, including the sequences and , which describe the full board and the empty board, respectively.
The problems on this page are the property of the MAA's American Mathematics Competitions