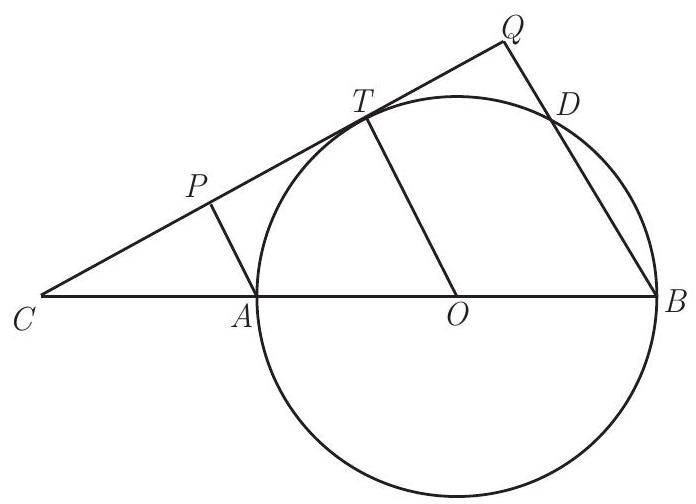
Problem:
Let AB be a diameter of circle ω. Extend AB through A to C. Point T lies on ω so that line CT is tangent to ω. Point P is the foot of the perpendicular from A to line CT. Suppose AB=18, and let m denote the maximum possible length of segment BP. Find m2.
Solution:
Let O be the center of the circle, and let Q be the foot of the perpendicular from B to line CT. Segment BQ meets the circle again (other than at B ) at D. Since AB is a diameter, ∠ADB=90∘ and ADQP is a rectangle. Then
BP2=PQ2+BQ2=AD2+BQ2=AB2−BD2+BQ2=AB2+(BQ−BD)(BQ+BD)=AB2+DQ(BQ+BD)
Note that ABQP is a trapezoid with OT as its midline. Hence AB= 2OT=AP+BQ=DQ+BQ. Consequently
BQ+BD=BQ+BQ−DQ=2BQ−DQ=2(BQ+DQ)−3DQ=2AB−3DQ
Combining the above shows that
BP2=AB2+DQ(2AB−3DQ)=AB2+124⋅(3DQ)(2AB−3DQ).
For real numbers x and y,4xy≤(x+y)2. Hence
BP2≤AB2+12(3DQ+2AB−3DQ)2=34AB2=31296, which equals 432.
This maximum may be obtained by setting 3DQ=2AB−3DQ, or 3PA= 3DQ=AB=2OT. It follows that COAC=OTPA=32, implying that CA=AB.
OR
Let ∠ABQ=α. Let R be on BQ such that OR⊥BQ. Let r be the radius of the circle. To maximize BP2, observe that BP2=PQ2+BQ2, and from △BRO it follows that OR=rsinα and BR=rcosα. Thus PQ=2rsinα, and BQ=r+rcosα. Then
PB2=(2rsinα)2+(r+rcosα)2=r2+r2(4sin2α+1+2cosα+cos2α)=r2(5−3cos2α+2cosα)=−3r2(−35+cos2α−32cosα)=−3r2((cosα−31)2−916).
The maximum for PB2 is thus attained when cosα=31 and has the value 92(16/3)=432.
Query: Segment BP reaches its maximum length when lines AD,BP, and OT are concurrent. Why?
The problems on this page are the property of the MAA's American Mathematics Competitions