Problem:
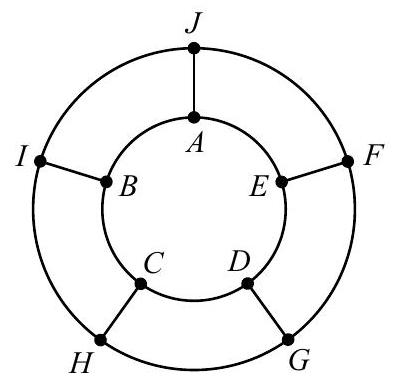
The wheel shown below consists of two circles and five spokes, with a label at each point where a spoke meets a circle. A bug walks along the wheel, starting at point . At every step of the process, the bug walks from one labeled point to an adjacent labeled point. Along the inner circle the bug only walks in a counterclockwise direction, and along the outer circle the bug only walks in a clockwise direction. For example, the bug could travel along the path , which has steps. Let be the number of paths with steps that begin and end at point . Find the remainder when is divided by .
Solution:
Let represent a step that is either counterclockwise or inward along a spoke, and let represent a step that is either clockwise or outward along a spoke. Then there is a one-to-one correspondence between the paths with steps starting at point and sequences of and in which the total number of and is . Furthermore, because there are five points on each circle, the bug ends at point if and only if the last move is an and the difference between the number of and the number of is a multiple of . Thus the bug ends at point if and only if, among the first moves, there are either , or and the last move is an . Therefore the number of paths beginning and ending at is
The requested remainder when is divided by is .
The problems on this page are the property of the MAA's American Mathematics Competitions