Problem:
A basketball player has a constant probability of of making any given shot, independent of previous shots. Let be the ratio of shots made to shots attempted after shots. The probability that and for all such that is given to be , where , and are primes, and , , and are positive integers. Find
Solution:
Let be the number of attempts and the number of shots made. The maximum values of for are , and , respectively. Since when , the minimum values of when are , respectively. We can represent the possible sequences of made and missed shots in the diagram below.
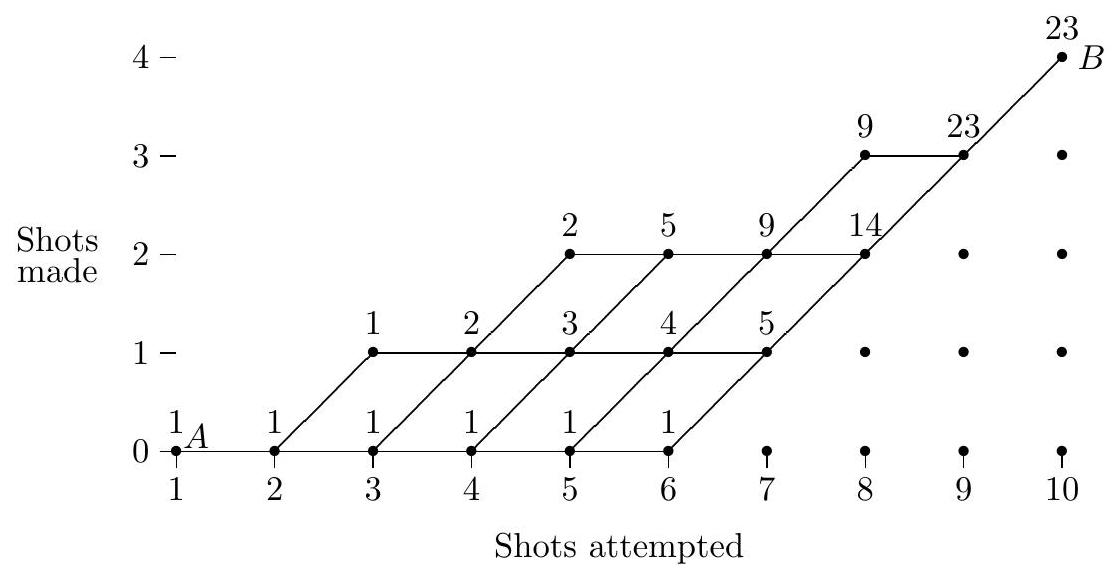
The possible sequences of made and attempted shots correspond to sequences of ordered pairs , where is the number of shots attempted and is the number of shots made, beginning at and ending at . Each sequence corresponds to a path from to that moves right and/or up on the lines in the diagram. The number of paths from to any point on the diagram is the sum of the number of paths from to the points directly before . Each point is labeled with the number of possible paths from to that point. Thus, the number of paths from to is . Each path represents a sequence of made shots and misses, so the requested probability is
and .
The problems on this page are the property of the MAA's American Mathematics Competitions