Problem:
Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between a.m. and a.m., and stay for exactly minutes. The probability that either one arrives while the other is in the cafeteria is , and , where , and are positive integers, and is not divisible by the square of any prime. Find .
Solution:
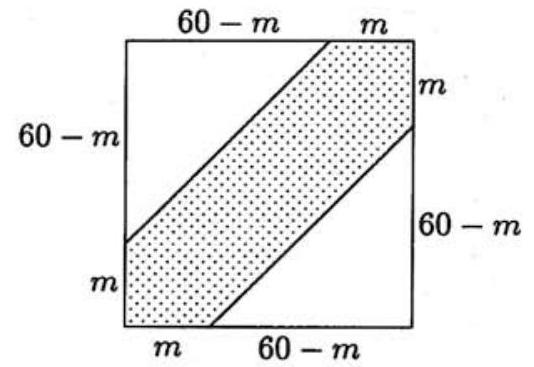
In the figure below, points in the square correspond to ordered pairs of arrival times, with and . The shaded points correspond to meetings, which occur if and only if . The probability of no meeting is , which is the ratio of the unshaded region to the area of the whole square. Thus , whose solutions are . Because must be smaller than , it follows that (about minutes), and .
The problems on this page are the property of the MAA's American Mathematics Competitions