Problem:
A wooden cube, whose edges are one centimeter long, rests on a horizontal surface. Illuminated by a point source of light that is centimeters directly above an upper vertex, the cube casts a shadow on the horizontal surface. The area of the shadow, which does not include the area beneath the cube, is square centimeters. Find the greatest integer that does not exceed .
Solution:
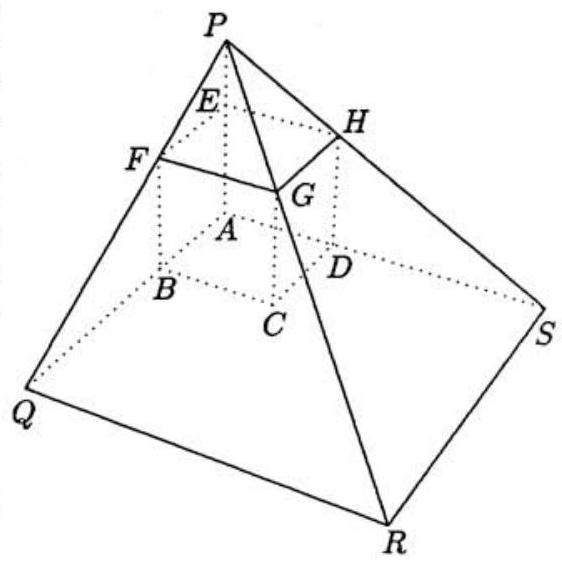
Let be the cube, be the point source of light, , and . In the diagram at right, , and are collinear, and , and are the intersections of the extensions of , and , respectively, with the plane of . Because the squares and are in parallel planes, it follows that pyramids and are similar. Therefore is a square, and
Solve this equation to obtain .
The area of the shadow is , hence
Thus and .
The problems on this page are the property of the MAA's American Mathematics Competitions