Problem:
The numbers , and are randomly written on the faces of a regular octahedron so that each face contains a different number. The probability that no two consecutive numbers, where and are considered to be consecutive, are written on faces that share an edge is , where and are relatively prime positive integers. Find .
Solution:
It is helpful to consider the cube shown in the figure. The vertices of the cube represent the faces of the dotted octahedron, and the edges of the cube represent adjacent octahedral faces. Each assignment of the numbers , and to the faces of the octahedron corresponds to a permutation of , and thus to an octagonal circuit of these vertices. The cube has diagonal segments that join nonadjacent vertices. In effect, the problem asks one to count octagonal circuits that can be formed by eight of these diagonals. Six of the diagonals are edges of tetrahedron , six are edges of tetrahedron , and four are long, joining a vertex of one tetrahedron to the diagonally opposite point from the other. Notice that each vertex belongs to exactly one long diagonal. It follows that an octagon cannot have two successive long diagonals. Also notice that an octagonal path can jump from one tetrahedron to the other only along one of the long diagonals. it follows that an octagon must contain either long diagonals separated by tetrahedron edges or long diagonals alternating with tetrahedron edges. To form an octagon that contains four long diagonals, choose two opposite edges from tetrahedron and two opposite edges from tetrahedron . For each of the three ways to choose a pair of opposite edges from tetrahedron , there are two possible ways to choose a pair of opposite edges from tetrahedron . There are distinct octagons of this type and ways to describe each of them, making permutations. To form an octagon that contains exactly two of the long diagonals, choose a three-edge path along tetrahedron , which can e done in ways. Then choose a three-edge path along tetrahedron which, because it must start and finish at specified vertices, can be done in only ways. Since this counting method treats each path as different from its reverse, there are permutations of this type. In all, there are permutations that correspond to octagonal circuits formed exclusively from cube diagonals.
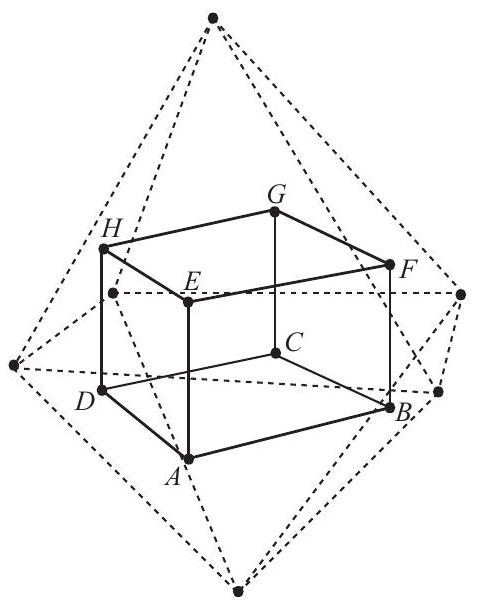
The probability of randomly choosing such a permutation is .
Note: The cube is called the emphdual of the octahedron.
The problems on this page are the property of the MAA's American Mathematics Competitions