Problem:
The shortest distances between an interior diagonal of a rectangular parallelpiped (box), , and the edges it does not meet are and . Determine the volume of .
Solution:
In order to find the volume of , we will determine its dimensions, and . To this end, consider the rectangular parallelepiped shown in the first figure below, with vertices and side lengths as indicated. For definiteness, we labeled the box so that
where, in general, denotes the distance between lines and .
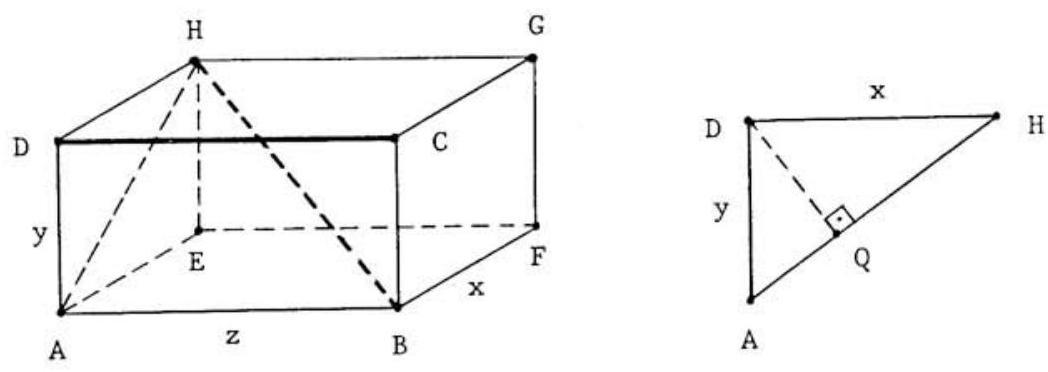
Now the distance from to is equal to the distance from to the plane , which is the same as the length of the perpendicular from to the diagonal of rectangle . To see this, note that this perpendicular is also perpendicular to the plane and the line . If one "slides" it over so that its top moves from towards , it eventually intersects line . This gives an equally long segment, which is perpendicular to both and , so its length is indeed the distance . This distance is found via similar triangles, as shown in the second figure above, in which , and hence . Treating the other distances similarly, in view of , this leads to the equations
Upon squaring each equation in , taking reciprocals and simplifying, one arrives at the system
We solve by first adding the equations therein, and then subtracting from times the resulting equation each of the original equations in . Thus we find that and . From these, and . Consequently, the volume of is .
The problems on this page are the property of the MAA's American Mathematics Competitions