Problem:
A machine-shop cutting tool has the shape of a notched circle, as shown. The radius of the circle is , the length of is and that of is . The angle is a right angle. Find the square of the distance (in centimeters) from to the center of the circle.
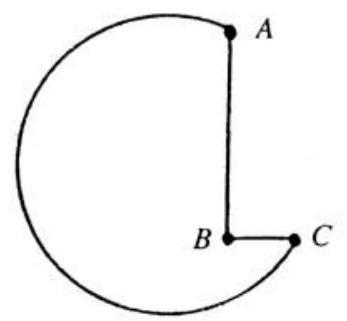
Solution:
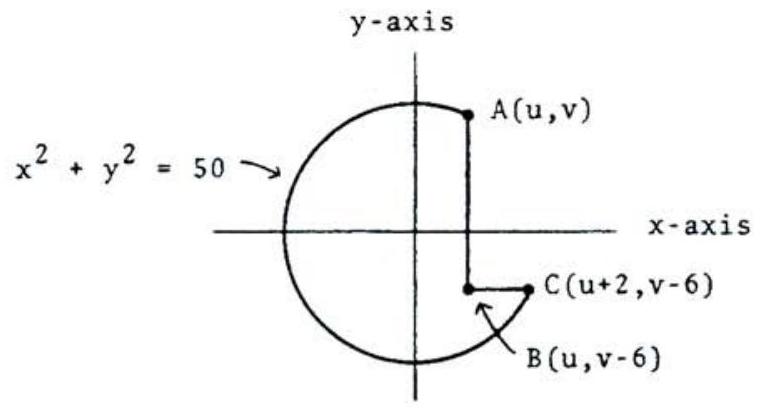
We introduce a coordinate system as shown in the figure: WLOG (Without Loss Of Generality) we have put the top corner of the notch in the First Quadrant and have positioned the sides of the notch parallel to the axes. Letting it follows, using the given dimensions, that and . Our problem is to determine . Since and are both on the circ1e , we may substitute their coordinates into this equation to, get the system
Subtracting the first equation from the second leads to . Solving for and substituting into the first equation gives
Since is in the First Quadrant, we have and . Finally, the square of the distance from to the origin is .
The problems on this page are the property of the MAA's American Mathematics Competitions