Problem:
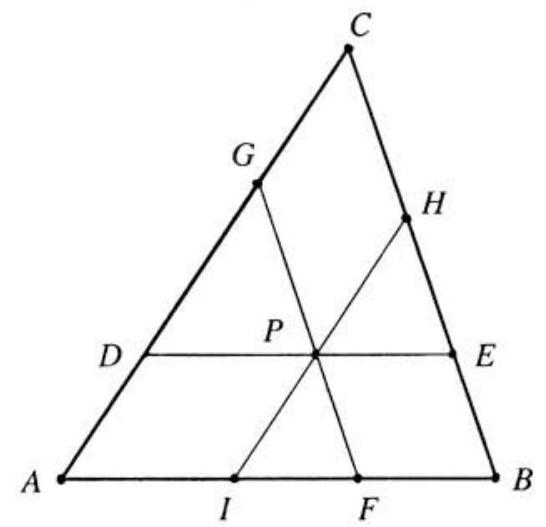
In â–³ABC shown below, AB=425,BC=450 and CA=510. Moreover, P is an interior point chosen so that the segments DE,FG and HI are each of length d, contain P, and are parallel to the sides AB,BC and CA, respectively. Find d.
Solution:
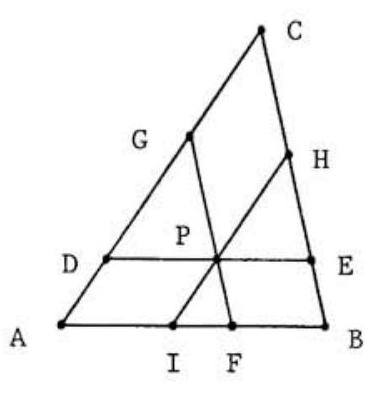
As shown in the figure on the right, EH=BC−(BE+HC)=BC−(FP+PG)=450−d.
In like manner, GD=510−d. Moreover, from the similarity of △DPG and △ABC we have GDDP​=CAAB​. Hence
DP=CAAB​⋅GD=510425​(510−d)=425−65​d(1)
In like manner, since â–³PEH and â–³ABC are similar, PE/EH=AB/BC. Hence
PE=BCAB​⋅EH=450425​(450−d)=425−1817​d(2)
Since d=DP+PE, adding (1) and (2) we find that d=850−916​d, from which d=306​.
The problems on this page are the property of the MAA's American Mathematics Competitions
