Problem:
Patio blocks that are regular hexagons unit on a side are used to outline a garden by placing the blocks edge to edge with on each side. The diagram indicates the path of blocks around the garden when .
If , then the area of the garden enclosed by the path, not including the path itself, is square units, where is a positive integer. Find the remainder when is divided by .
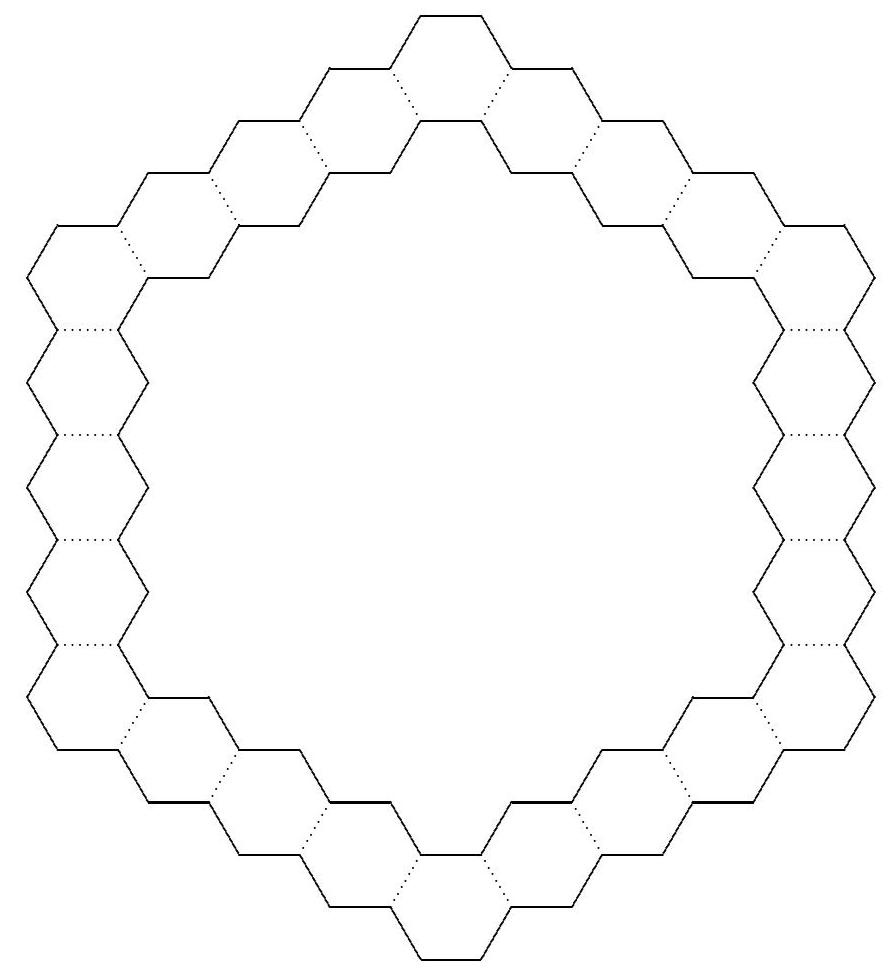
Solution:
The garden can be partitioned into regular hexagons congruent to the blocks, and the hexagons on the boundary of the garden form a figure like the path, but with only hexagons on a side.
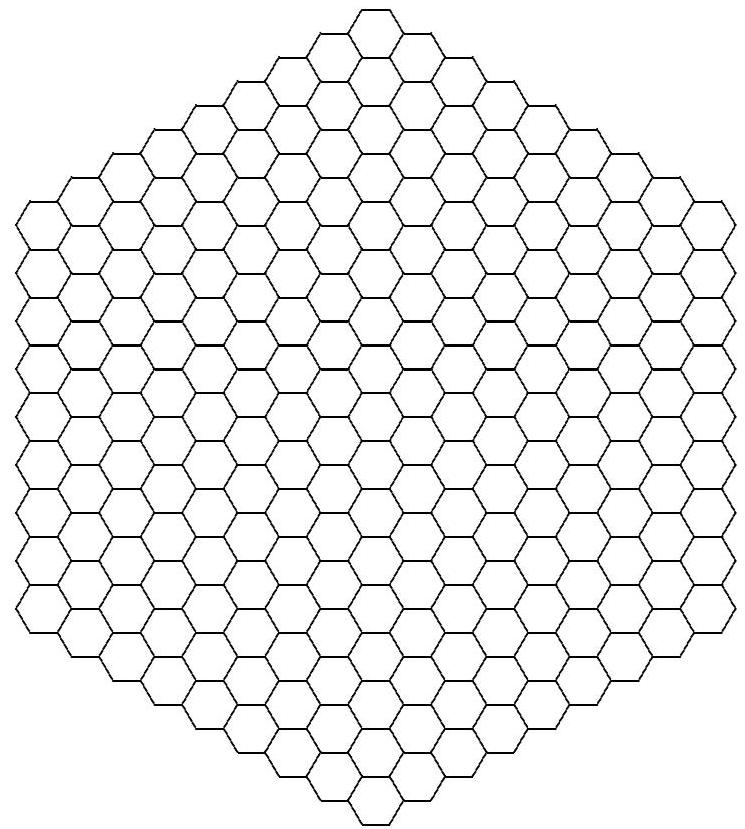
The figure shows the garden (not including the walk) when . Note that for any , counting the hexagons by columns starting at the left, each column contains one more hexagon than the column adjacent to it on the left, until the center column is reached. Since the leftmost column contains hexagons and the longest column is the to the right of it, the longest column contains hexagons. The number of hexagons strictly to the left of the center vertical line is therefore
and there are the same number to the right. Since the area of each of the hexagons is six times the area of an equilateral triangle of side , the area of the garden is
When this is square units, so the desired remainder is .
For , note that when there are hexagons per side of the bounding path, there is a total of hexagons on the path. The number of hexagons in the interior of the path is
so when , the garden can be partitioned into hexagons. Since the area of each hexagon is , the area of the garden is .
The problems on this page are the property of the MAA's American Mathematics Competitions