Problem:
In a regular tetrahedron, the centers of the four faces are the vertices of a smaller tetrahedron. The ratio of the volume of the smaller tetrahedron to that of the larger is , where and are relatively prime positive integers. Find .
Solution:
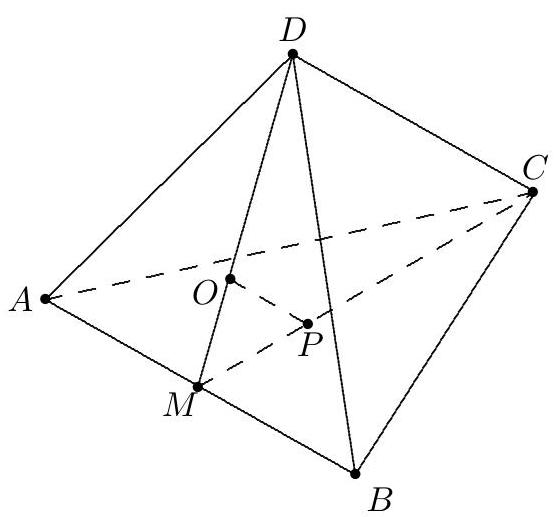
Let and be the centers of faces and , respectively, of regular tetrahedron . Both and intersect at its midpoint . Since , triangles and are similar, and . Because the tetrahedra are similar, the ratio of their volumes is the cube of the ratio of a pair of corresponding sides, namely, , so .
The problems on this page are the property of the MAA's American Mathematics Competitions