Problem:
The two squares shown share the same center and have sides of length . The length of is and the area of octagon is , where and are relatively prime positive integers. Find .
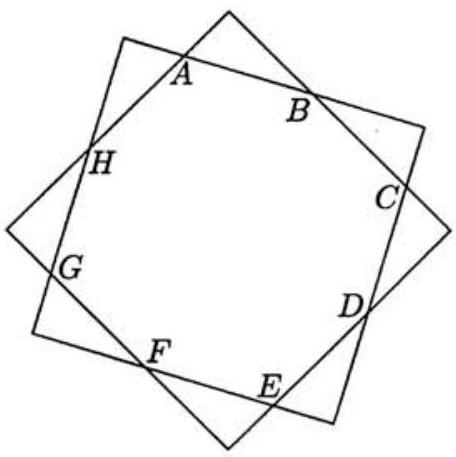
Solution:
Notice that is the center of the circle in which both squares are inscribed. The reflection of either square across the diameter determined by is another square inscribed in the same circle. Because the circle has only two chords of length that go through , the squares must be reflected images of each other. In particular, . Similar reasoning shows that any two adjacent sides of have the same length, so the octagon is equilateral. Because the distance from to all eight sides of the squares is , the area of the octagon is eight times the area of triangle ; i.e., . Thus .
Let be that vertex of one of the squares for which angle is right, and let and . Then
Hence
Because is the combined area of the four corner triangles, the area of the octagon is , and .
Query: Could this problem have been posed with the hypothesis ?
The problems on this page are the property of the MAA's American Mathematics Competitions