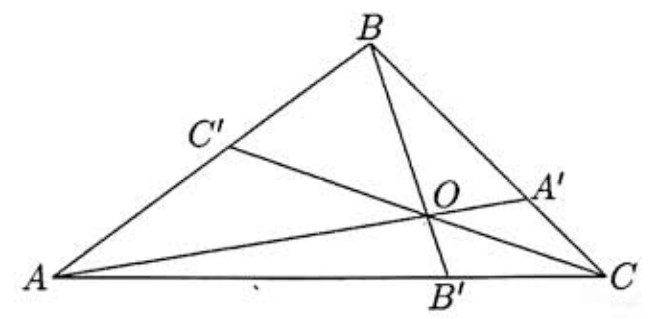
Problem:
In triangle ABC,A′,B′, and C′ are on sides BC,AC, and AB, respectively. Given that AA′,BB′, and CC′ are concurrent at the point O, and that
OA′AO+OB′BO+OC′CO=92
find the value of
OA′AO⋅OB′BO⋅OC′CO
Solution:
Since △AOB and △A′OB share an altitude, as do △AOC and △A′OC, we have
OA′AO=[A′OB][AOB]=[COA′][COA]=[A′OB]+[COA′][AOB]+[COA]=[BOC][AOB]+[COA]=xz+y
where x=[BOC],y=[COA], and z=[AOB]. Similarly,
OB′BO=yx+z and OC′CO=zy+x
We then have
OA′AOOB′BOOC′CO=xyz(z+y)(x+z)(y+x)=xyzyz2+y2z+x2z+xz2+xy2+x2y+2xyz=xyzyz(z+y)+xz(x+z)+xy(y+x)+2=xz+y+yx+z+zy+x+2
Hence,
OA′AOOB′BOOC′CO=(OA′AO+OB′BO+OC′CO)+2=92+2=94
The problems on this page are the property of the MAA's American Mathematics Competitions