Problem:
Two real numbers and are chosen independently and uniformly at random from the interval . Let and be two points in the plane with . Let and be points on the same side of line such that the degree measures of and are and , respectively, and and are both right angles. The probability that is equal to , where and are relatively prime positive integers. Find .
Solution:
Because and are on the same side of line and , points , and lie on a semicircle with diameter , as shown. Because the radius of the semicircle is , the length of chord is less than or equal to if and only if the arc of the semicircle between and has central angle of no more than . This happens exactly when the inscribed angle does not exceed ; that is .
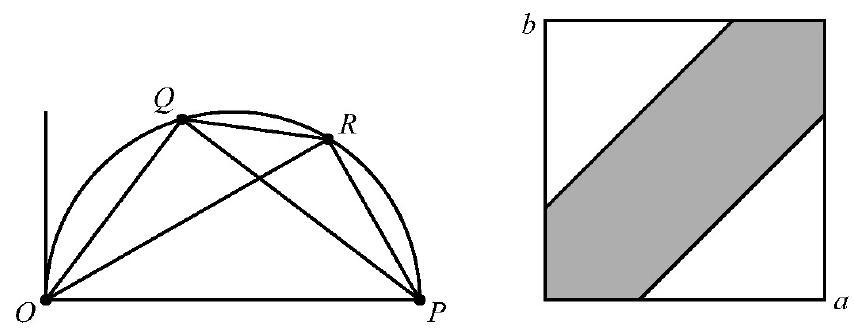
Each pair of values and corresponds to a unique point in the -plane, with and , and vice versa. The points in the -plane that meet the requirement are those within the square that satisfy the relation , that is, the shaded hexagonal region within the square, as shown. The two triangles inside the square and outside the hexagon are both isosceles right triangles with leg length . Hence the requested probability is . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions